HARMONIQUE ANALYSE
La transformation de Fourier
Certaines classes importantes de fonctions ne se prêtent pas à l'analyse harmonique telle qu'elle a été définie ci-dessus. Ainsi, l'espace L1(R) des (classes de) fonctions intégrables sur R ne contient aucune exponentielle ; aussi utilise-t-on un autre procédé pour en faire l'analyse et la synthèse. C'est la transformation de Fourier qui permet de définir le spectre d'une fonction intégrable et, dans certains cas, d'en faire la synthèse.
Soit f une fonction intégrable (par exemple, continue et nulle hors d'un ensemble borné). À f on associe une autre fonction définie sur R, notée f̂ ou Ff, et appelée transformée de Fourier de f :
La présence du coefficient − 2π est conventionnelle (la convention n'est d'ailleurs pas universelle) et permet d'avoir une formule de réciprocité particulièrement simple.
Définissons, outre l'opérateur F de transformation de Fourier, l'opérateur F− de transformation de Fourier conjuguée (ou réciproque) :
Pour toute fonction f, et tout réel t, on a :
Propriétés de la transformation de Fourier
a) Pour toute fonction intégrable f, Ff est continue et tend vers 0 à l'infini. Si on désigne par A(R) l'ensemble des fonctions Ff, pour f ∈ L1(R), A(R) est donc un sous-espace de l'espace vectoriel C0(R) des fonctions continues sur R qui tendent vers 0 à l'infini. En fait, A(R) est strictement plus petit que C0(R). b) Si f et g sont intégrables, leur produit de convolution f * g, défini par :
On a alors :
Il est intéressant de voir comment certaines propriétés des fonctions se traduisent sur leurs transformées de Fourier.
Par exemple, les relations (8) et (9) montrent que plus une fonction est régulière (dérivable), plus sa transformée de Fourier tend rapidement vers 0 à l'infini. Inversement, plus f tend rapidement vers 0 à l'infini, plus Ff est régulière. Voici un autre exemple, présenté en termes vagues : plus les valeurs d'une fonction sont concentrées autour de l'origine, plus celles de sa transformée de Fourier sont, au contraire, étalées.
Le théorème de réciprocité
De même que la série de Fourier d'une fonction périodique caractérise celle-ci, sans qu'aucune propriété de convergence soit nécessaire, la transformée de Fourier d'une fonction f caractérise cette fonction. Donc la donnée de Ff contient toute l'information relative à f. Dans certains cas, il est possible d'exprimer f explicitement à partir de Ff.
Théorème. Si f et Ff sont toutes deux intégrables, on a :
C'est là une remarquable propriété de symétrie entre les opérateurs F et F−.
On peut encore interpréter cela comme une propriété de synthèse : si on appelle spectre de f le support de sa transformée de Fourier Ff, c'est-à-dire l'adhérence de l'ensemble des points où Ff ne s'annule pas, le théorème de réciprocité, lorsque Ff est intégrable, s'écrit :
Une classe très importante[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
Écrit par
- René SPECTOR : professeur à l'université d'Orléans
Classification
Pour citer cet article
René SPECTOR. HARMONIQUE ANALYSE [en ligne]. In Encyclopædia Universalis. Disponible sur : (consulté le )
Autres références
-
ANALYSE MATHÉMATIQUE
- Écrit par Jean DIEUDONNÉ
- 8 527 mots
Un autre type de groupe de transformations est fourni par le cas où la variété où opère le groupe est un espace vectoriel complexe E, et où les transformations sont linéaires ; lorsqu'un groupe G agit de cette façon sur E, on dit encore qu'on a une représentation linéaire de G. -
CALCUL ET RATIONALISATION - (repères chronologiques)
- Écrit par Pierre MOUNIER-KUHN
- 725 mots
1623 L'astronome allemand Wilhelm Schickard invente une « horloge à calcul ». Mais celle-ci disparaît dans un incendie et Schickard ne poursuit pas ce projet qui n'aura donc aucune influence historique.
1637 René Descartes, dans le Discours de la méthode, définit la méthode rationnelle...
-
CARLESON LENNART (1928- )
- Écrit par Universalis, Jeremy John GRAY
- 766 mots
Le mathématicien suédois Lennart Carleson reçut en 2006 le prix Abel « pour ses contributions profondes et déterminantes à l'analyse harmonique et à la théorie des systèmes dynamiques lisses ». Cette récompense couronne notamment les travaux effectués avec son collègue et compatriote...
-
FONCTIONS REPRÉSENTATION & APPROXIMATION DES
- Écrit par Jean-Louis OVAERT, Jean-Luc VERLEY
- 18 453 mots
- 6 médias
Dans les problèmes d'analyse harmonique des phénomènes non périodiques (cf. analyse harmonique, chap. 3), on utilise la transformation de Fourier, réelle ou complexe, définie par la relation :(ou des formes analogues selon les auteurs), et la formule d'inversion :
intuitivement, la formule...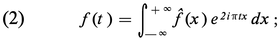
- Afficher les 13 références
Voir aussi
- CORDES VIBRANTES
- BERNOULLI DANIEL (1700-1782)
- CONVOLUTION PRODUIT DE
- CONVERGENCE, mathématiques
- CARACTÈRE, mathématiques
- GROUPE TOPOLOGIQUE
- HAAR MESURE DE
- FOURIER SÉRIE DE
- DUAL D'UN GROUPE
- FOURIER TRANSFORMATION DE
- GROUPE COMMUTATIF ou GROUPE ABÉLIEN
- CESARO MOYENNES DE
- BESSEL-PARSEVAL-PLANCHEREL THÉORÈME DE
- PRESQUE PÉRIODIQUE FONCTION
- SPECTRE D'UNE FONCTION
- PARSEVAL IDENTITÉ DE
- PONTRIAGUINE-VAN KAMPEN THÉORÈME DE DUALITÉ DE
- PÉRIODIQUE FONCTION
- HARMONIQUE SYNTHÈSE
- FOURIER-PLANCHEREL TRANSFORMATION DE
- FOURIER COEFFICIENTS DE
- INTÉGRABLES ESPACES DE FONCTIONS
- DISTRIBUTIONS TEMPÉRÉES
- FEJÉR LEOPOLD (1880-1959)
- DUALITÉ, mathématiques
- GROUPE LOCALEMENT COMPACT
