ANNEAUX & ALGÈBRES

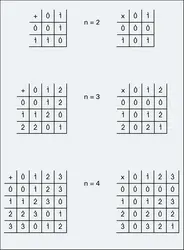
Anneaux de Boole

L'exemple suivant montre le caractère un peu insolite que peuvent présenter certains anneaux. L'ensemble P (E) des parties d'un ensemble donné E est un anneau pour les opérations d'« addition » et de « multiplication » qui à deux sous-ensembles X et Y de E font correspondre les sous-ensembles :

Revenons aux notations usuelles en désignant les éléments d'un anneau par des lettres minuscules. Généralisant la situation précédente, on considère des anneaux, appelés anneaux de Boole, qui possèdent la propriété que le carré de tout élément est égal à cet élément : x²= xx = x. Il en résulte que, pour tout élément x, on a x + x = 0 ; en effet, écrivant que le produit de x + x par lui-même est égal à x + x, on obtient :

Anneaux et algèbres de fonctions

Les fonctions réelles d'une variable réelle définies dans un intervalle[a, b]de la droite réelle constituent une algèbre en convenant que la somme et le produit de deux fonctions ou le produit d'une fonction par un nombre réel λ sont les fonctions dont les valeurs en chaque point sont respectivement la somme et le produit des valeurs en ce point ou le produit par λ de la valeur de la fonction en ce point. Si on analyse les propriétés qui ont permis de munir l'ensemble précédent d'une structure d'algèbre, on constate que, de manière générale, on peut munir d'une structure d'anneau ou d'algèbre l'ensemble des applications d'un ensemble quelconque E dans un anneau ou une algèbre respectivement, les valeurs en un point x de E des fonctions somme, produit et éventuellement produit par un scalaire étant données par :

Le procédé précédent permet, bien entendu, de définir des structures d'anneaux ou d'algèbres sur de nombreux ensembles de fonctions contenus dans l'ensemble, considéré ci-dessus, de toutes les fonctions définies dans un ensemble et à valeurs dans un anneau ou une algèbre. Ainsi, les fonctions continues ou différentiables à valeurs réelles définies dans un ouvert du plan constituent des algèbres sur le corps des nombres réels. Il est clair qu'il est possible de multiplier à volonté les exemples de ce type.

Lorsqu'on s'intéresse à l'étude locale des fonctions au voisinage d'un point, on est conduit à introduire des anneaux et algèbres d'un type différent du précédent. Nous prendrons pour exemple l'algèbre des germes de fonctions analytiques à l'origine O du plan complexe. Considérons les couples (U, f ) d'un voisinage ouvert de O dans le plan complexe et d'une fonction f définie et analytique dans U. Nous dirons que deux tels couples (U, f ) et (V, g) définissent le même germe à l'origine si f et g coïncident sur un voisinage ouvert W de O contenu dans U ∩ V ; il est clair que cette relation est une relation d'équivalence ; par définition, le germe d'une fonction analytique définie dans un voisinage de O est sa classe d'équivalence pour cette relation. Montrons que cet ensemble des germes peut être muni d'une structure d'algèbre sur le corps des nombres réels ou des nombres complexes. Soient A et B deux germes et λ un nombre réel ou complexe. Si (U, f ) et (V, g) définissent les germes A et B respectivement, nous appellerons germe somme, germe produit et germe produit par le scalaire λ, noté A + B, AB et λA respectivement, les germes à l'origine des couples (U ∩ V, f₁+ g₁), (U ∩ V, f ₁g₁), et (U ∩ V, λf₁), où f₁ et g₁ désignent les restrictions au voisinage U ∩ V des fonctions f et g ; on vérifie alors facilement que les germes A + B, AB et λA sont indépendants des représentants (U, f ) et (V, g) choisis et que l'ensemble des germes est ainsi muni d'une structure d'algèbre. De manière générale, les anneaux de germes de fonctions différentiables ou analytiques jouent un rôle absolument essentiel dans la théorie des variétés différentiables ou analytiques.

Anneaux de séries

A étant un anneau commutatif, on peut définir de manière purement formelle et algébrique des séries à coefficients dans A ; dans le cas où A est le corps des nombres complexes ou des nombres réels, nous ferons jouer un rôle particulier à celles de ces séries, dites convergentes, qui possèdent un rayon de convergence non nul.

On appelle série formelle (à une variable) à coefficients dans un anneau commutatif A une suite infinie d'éléments de A : (a₀, a₁, ..., a_n,...) ; une telle série formelle est souvent notée :

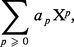
Il est facile maintenant de vérifier, en utilisant les règles du calcul algébrique dans les anneaux, que l'ensemble A [[X]] de ces séries formelles est muni d'une structure d'anneau ; si A = K est un corps, cet anneau est une algèbre quand on définit la multiplication scalaire par la formule :

Par récurrence, on peut définir l'anneau des séries formelles à n variables à coefficients dans A ; par définition, cet anneau, noté A [[X₁, ..., X_n]], est égal à l'anneau des séries formelles (à une variable) à coefficients dans l'anneau A [[X₁, ..., X_n-1]] des séries formelles à (n − 1) variables. Toute série formelle à n variables est définie par la donnée, pour tout système de n entiers p₁, ..., p_n positifs ou nuls, d'un élément a_{p1 ... pn} de l'anneau A et s'écrit symboliquement sous la forme :

Limitons-nous maintenant au cas où A est le corps des nombres réels ou des nombres complexes. La série (_*) est dite convergente si elle a un rayon de convergence non nul, c'est-à-dire s'il existe un nombre réel strictement positif R tel que la famille de nombres positifs :

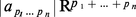
Algèbres de dimension finie

Soit A une algèbre sur un corps K dont l'espace vectoriel sous-jacent soit de dimension finie n et choisissons une base e₁, ..., e_n de cet espace. On appelle table de multiplication de A la donnée des produits :

Réciproquement, soit E un espace vectoriel muni d'une base e₁, ..., e_n. Si on se donne, pour tout couple i, j d'entiers compris entre 1 et n, des éléments de l'espace E, notés e_ie_j, on peut prolonger cette loi par bilinéarité à l'espace E tout entier. L'espace E est alors une algèbre associative admettant cette loi pour multiplication si, et seulement si, on a (e_ie_j) e_k = e_i(e_je_k) ; remarquons que l'algèbre ainsi construite est commutative si, et seulement si, e_ie_j = e_je_i. Ce qui précède montre l'utilité des tables pour définir des algèbres. Nous allons donner un exemple célèbre de cette situation.

Soit K un corps commutatif ; désignons par e, i, j, k la base canonique de l'espace vectoriel K⁴ et choisissons deux éléments p et q de K. On appelle algèbre de quaternions sur K l'algèbre obtenue en considérant sur K⁴ la table de multiplication notée H :

Un cas particulier très important s'obtient en prenant pour K le corps des nombres réels et en choisissant p = q = − 1 ; on obtient ainsi les quaternions proprement dits, introduits par Hamilton. Pour ces quaternions, on peut développer une théorie analogue à celle des nombres complexes : si x = ae + bi + cj + dk est un tel quaternion, on appelle conjugué de x le quaternion x̄ = ae − bi − cj − dk ; les règles de calcul montrent alors que :

Pour terminer, remarquons que les matrices de la forme :