NUMÉRIQUE CALCUL

Méthode de dichotomie

Soit g une fonction numérique continue et strictement monotone sur un intervalle[a, b], telle que g (a)g (b) < 0. Il existe alors un élément α de[a, b]et un seul tel que g (α) = 0. On peut trouver des valeurs approchées de α par l'algorithme suivant : supposons par exemple g (a) > 0 et g (b) < 0 ; posons a₀ = a, b₀ = b, et :

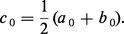
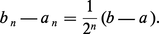
Dès le xvi^e siècle, cette méthode est employée pour séparer les racines d'une équation algébrique. La convergence n'est pas très rapide ; c'est pourquoi cette méthode n'est pas utilisée lorsqu'on désire obtenir α avec une grande précision.

En revanche, le méthode de dichotomie a eu une importance considérable dans le développement des concepts fondamentaux de l'analyse :

– Lagrange (1736-1813), dans La Théorie des fonctions analytiques (1797), utilise une variante de cette méthode pour démontrer le principe fondamental du calcul différentiel, suivant lequel une fonction admettant une dérivée positive est croissante ; ce principe est à la base de la formule de Taylor.

– Bolzano (1781-1848), dans Une preuve analytique... (1817) et Cauchy (1789-1857), dans son Cours d'analyse à l'École polytechnique (1821), utilisent la dichotomie pour démontrer le théorème des valeurs intermédiaires.

– L'école de Weierstrass (1815-1897) utilise systématiquement la dichotomie pour démontrer les théorèmes fondamentaux sur les fonctions continues (existence d'un maximum, continuité uniforme). Ces résultats reposent sur le théorème suivant, dit de Bolzano-Weierstrass : de toute suite bornée de nombres réels, on peut extraire une suite convergente.

Méthode d'interpolation linéaire (ou « regula falsi »)

Sous les mêmes hypothèses que précédemment, on cherche une valeur approchée β de ω en interpolant g sur l'intervalle[a,b]par une fonction affine ϕ, et en définissant β par la relation ϕ(β) = 0. Cette méthode a été utilisée par Viète (1540-1603) et par Descartes (1596-1650), dans le cas des équations algébriques. La majoration de l'erreur a été effectuée par Lagrange.

Cette méthode est peu employée seule car elle ne conduit pas à un processus itératif qui soit à la fois commode et performant.

Méthode des tangentes (ou de Newton)

L'école d' Alexandrie, et en particulier Archimède, utilise fréquemment des encadrements des racines carrées d'un nombre entier par des nombres rationnels. À cet effet, on utilise l' algorithme d'Euclide de divisions successives. Héron d'Alexandrie part d'une autre idée. Pour approcher √ a, il écrit a sous la forme a = r² + b, où r est le plus grand des entiers p tels que p² ≤ a. Ainsi, √ a = r √1 + (b/r²). Il approche √1 + (b/r²) par 1 + (b/2r²). D'où la valeur approchée suivante :

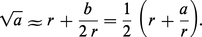
On itère alors ce processus. Plus précisément, on pose :

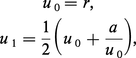
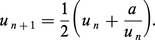
Cette rapidité peut être prévue grâce aux encadrements suivants : on prouve d'abord que |u₂ − √2| ≤ 1/400. Par ailleurs, pour tout entier naturel n,

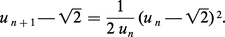
En particulier, u₄ et u₅ fournissent respectivement des approximations de √2 à 10^-11 près et à 10^-23 près.

Cette méthode est incomparablement supérieure à la méthode encore enseignée (pour des raisons inconnues) dans les lycées et collèges français, laquelle repose sur une décomposition en tranches de deux chiffres.

La méthode de Héron est reprise par Newton dans son traité Principes mathématiques de la philosophie naturelle. Lors de l'étude du mouvement des planètes, il est amené à rechercher des solutions approchées de l'équation de Kepler x = a + e sin x, où e < 1. Plus généralement, pour chercher des solutions approchées de l'équation g (x) = 0, on part d'une valeur initiale c et l'on prend pour valeur approchée l'abscisse b du point d'intersection avec Ox de la tangente au graphe de g au point d'abscisse c. On a :

Cette méthode est connue sous le nom de méthode de Newton-Raphson. Cauchy fut le premier à préciser les conditions portant sur g assurant la convergence du processus (Cours d'analyse paru en 1821).

La convergence est extrêmement rapide : on peut prouver qu'elle est de l'ordre de k⁽²ⁿ⁾. Il convient de remarquer que, si l'on applique la méthode de Newton à la résolution de l'équation x² − a = 0, on obtient précisément l'algorithme :

Méthode des approximations successives

Un autre problème célèbre, dû à Ptolémée (128-168), est celui de la recherche de valeurs approchées de sin 1⁰. (Ce problème apparaît dans la construction de tables trigonométriques.) Dans l'Almageste, Ptolémée calcule sin 72⁰ et sin 60⁰ ; il en déduit sin 12⁰ puis, par dichotomies successives, sin 1⁰ 30′ et sin 45′. Il effectue enfin une interpolation linéaire pour obtenir une valeur approchée de sin 1⁰. Cette méthode fournit une valeur approchée à 10 ^-6 près. Les progrès de l'astronomie ont amené les mathématiciens arabes à améliorer cette précision. Vers 1400, al- Kashi, astronome à l'observatoire de Samarcande, part de la relation sin 3 x = 3 sin x − 4 sin³ x. Connaissant sin 3⁰, il en déduit sin 1⁰, en résolvant par approximations successives l'équation :

On peut montrer a priori que le nombre u₃ fournit une approximation de sin 1⁰ à 10 ^-10 près. En effet,

Cette méthode est reprise par Viète en 1600 et par Wallis en 1660, pour la résolution des équations algébriques.

Là encore, c'est Cauchy qui a précisé les hypothèses assurant la convergence du processus. Voici l'énoncé général : soient I un intervalle fermé de R et f une application de I dans lui-même. On suppose que f est contractante, c'est-à-dire qu'il existe un nombre réel positif k strictement inférieur à 1 tel que, pour tout couple (x, y) de points de I,

Dans ces conditions, l'application f admet un point fixe a et un seul ; en outre, pour tout élément c de I, la suite (u_n), définie par les relations u_n + 1 = f (u_n) et u₀ = c, converge vers a. Enfin, pour tout entier naturel non nul p,

Supposons maintenant que l'on veuille résoudre par cette méthode une équation de la forme g (x) = 0, où g est de classe C¹ sur un intervalle J de R, sachant qu'il existe un élément α de J et un seul tel que g (α) = 0 ; on suppose en outre que g′(α) ≠ 0. L'idée consiste à écrire l'équation g (x) = 0 sous la forme f (x) = x, où :

Le cas idéal est celui où, à chaque pas de l'itération, f ″(u_n) est nul ; on peut s'y ramener en modifiant à chaque pas le facteur a. On obtient alors l'algorithme suivant pour résoudre l'équation g (x) = 0. On pose u₀ = c ; il convient donc de prendre a₀ = − g′(u₀). Par suite :

Néanmoins, lorsque l'expression de g′ est compliquée, la méthode de Newton est d'emploi peu commode. Il est alors préférable d'effectuer une accélération de convergence immuable.

La méthode des approximations successives, issue du calcul numérique, a été employée par Picard (1856-1941), pour la recherche des solutions des équations différentielles. Au cours du xx^e siècle, son champ d'application est élargi à tous les secteurs de l'analyse : équations implicites, équations aux dérivées partielles, traitement numérique des matrices, topologie algébrique, etc. On utilise à cet effet l'énoncé suivant : soit (A, d ) un espace métrique et f une application de A dans lui-même, telle que la série des rapports de Lipschitz λ( fⁿ) converge. Alors l'application f a un point fixe a et un seul. En outre, pour tout élément c de A, la suite (u_n) définie par les relations u_n + 1 = f (u_n) et u₀ = c converge vers a. Enfin, pour tout entier naturel non nul p,

Lorsque f est contractante, λ(fⁿ) ≤ kⁿ, et on retrouve le cas classique. Mais l'énoncé précédent est plus précis ; par exemple, dans le cas des équations différentielles, la convergence est d'ordre Mⁿ/n !.

Comparaison des méthodes précédentes

Il convient ici, comme dans tous les problèmes de calcul numérique, de distinguer trois niveaux :

– celui de l'existence et de l'unicité des solutions, problème d'analyse mathématique ;

– celui de la rapidité de convergence des processus d'approximation, problème d'analyse numérique ;

– celui de la performance du processus, c'est-à-dire du temps total (et donc du coût) nécessaire pour effectuer le calcul avec un matériel donné et une précision donnée, problème de calcul numérique et d'informatique.

Il faut en effet remarquer qu'un algorithme peut être plus rapidement convergent qu'un autre, tout en étant moins performant. Ainsi, la convergence d'un processus par trichotomie est d'ordre 1/3ⁿ, tandis que celle d'un processus par dichotomie est d'ordre 1/2ⁿ ; cependant, la dichotomie est plus performante car, à chaque pas, elle nécessite moins de calculs.

Bien entendu, lorsque le calcul de g′ est simple, la méthode de Newton est la plus performante. Dans le cas contraire, on emploie une méthode d'approximations successives (avec éventuellement accélération de convergence). Cependant, ces méthodes ne sont performantes que dans la mesure où la valeur initiale c est assez proche de la racine. Pour obtenir de telles valeurs, on utilise couramment une dichotomie ou une interpolation linéaire.