CONIQUES
Article modifié le
Les coniques à centre
Foyers
Pour les coniques à centre, les deux définitions métriques courantes sont les suivantes :
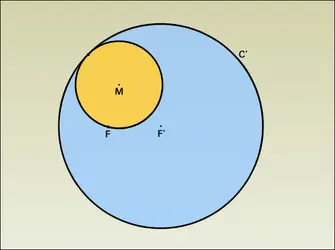
– l'ensemble des points M qui sont centre d'un cercle passant par un point donné F et tangent à un cercle donné C′ de centre F′ : définition bifocale ;
– l'ensemble des points M tels que la distance MF soit proportionnelle à la distance MH de M à la droite D (directrice associée à F) : définition monofocale.
La première met en jeu deux foyers, F et F′, et le cercle directeur C′ de centre F′ et de rayon (2a). Par hypothèse, FF′ = 2c est distinct de 2a (F n'appartient pas à C′). Si l'on peut écrire c < a, alors F est intérieur à C′ et la courbe obtenue, lieu de M tel que :

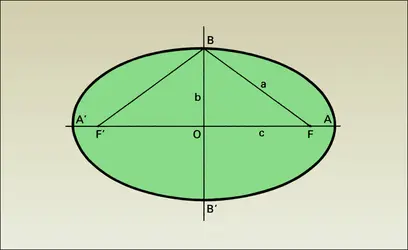
Ces coniques admettent deux axes de symétrie perpendiculaires (dont FF′, appelé axe focal) et un centre de symétrie O, milieu de FF′. L'axe focal coupe la courbe aux sommets A et A′, tels que :
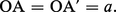
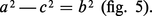
Tangentes
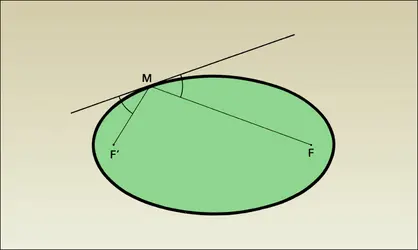
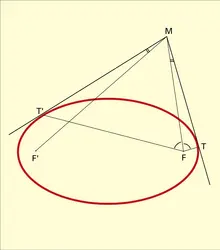
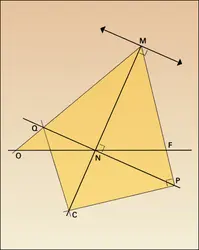
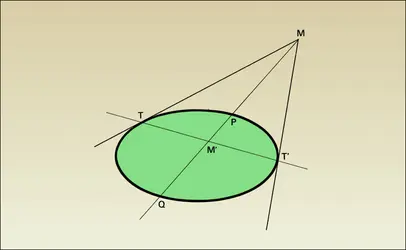
En chaque point d'une conique à centre il existe une tangente. Celle-ci est la bissectrice de l'angle géométrique FMF′ (extérieure pour l'ellipse, , intérieure pour l'hyperbole). On ne peut mener deux tangentes MT et MT′ distinctes à la conique que par un point M extérieur à celle-ci, défini par exemple par la relation MF > eMH, où e = c/a est l'excentricité de la conique (inférieure à 1 pour l'ellipse, égale à 1 pour la parabole par définition, et supérieure à 1 pour l'hyperbole). Sur la conique même (MF = eMH), ce qui est la seconde définition, il y a une tangente unique (double). D'un point intérieur (MF < eMH) on ne peut pas mener de tangentes ; c'est notamment le cas en F ou en F′. Si les tangentes existent, MT et MT′ ont mêmes bissectrices que MF et MF′ ; de plus FM est bissectrice de l'angle TFT′ (cf. , pour l'ellipse). MT est perpendiculaire à MT′ si M appartient au cercle de Monge, de centre O et de rayon √2a2 − c2 (pour e ≤ √2).
La projection de F sur une tangente décrit le cercle de diamètre AA′ ; si la projection de F sur une droite est dans la même région que F par rapport à ce cercle, la droite donnée coupe la conique en deux points distincts que l'on peut construire ; si la projection est dans l'autre région, la droite ne coupe pas la conique. On peut déduire de cela des définitions de l'ellipse et de l'hyperbole comme enveloppes de droites, comme pour la parabole.
Parmi les tangentes à une hyperbole, deux sont particulières. Issues de O, elles n'ont aucun point de contact à distance finie avec la courbe dont elles sont des asymptotes ; elles déterminent deux angles contenant chacun une branche connexe de l'hyperbole.
Correspondances linéaires
Si une tangente variable coupe deux tangentes fixes à une conique à centre, les abscisses x et x′ des deux points d'intersection sont reliées par une relation homographique du type :
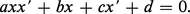
Il existe une réciproque importante à cette propriété affine : une droite joignant deux points de deux droites fixes dont les abscisses sont reliées par une telle relation (où a ≠ 0) enveloppe une conique à centre (a = 0 correspond à une parabole). Le produit des distances des deux foyers à une tangente variable est égale à b2 ; les foyers sont de part et d'autre pour une hyperbole, du même côté pour une ellipse. Certaines des propriétés précédentes s'étendent naturellement à une parabole, en supposant par exemple que la direction de F′ est celle de l'axe.
Pour que quatre points d'une conique soient sur un même cercle, il faut et il suffit que deux des cordes les joignant soient symétriques par rapport aux axes de la conique. D'un point du plan, on peut mener jusqu'à quatre normales à une conique à centre. Les pieds de trois d'entre elles et le point diamétralement opposé au quatrième sont sur un même cercle.
Si l'on se donne deux directions perpendiculaires, les points d'où les tangentes issues ont des directions symétriques par rapport à ces directions privilégiées appartiennent à une hyperbole (équilatère) de même centre que la conique, passant par les deux foyers ; il en serait de même si l'on remplaçait les deux directions choisies par celles de leurs bissectrices, d'où la position des foyers à l'intersection des deux hyperboles.
Propriétés différentielles et intégrales
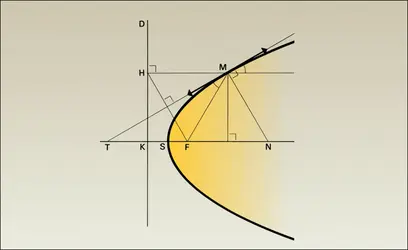
La normale en M coupe l'axe focal en N tel que NF = eMF. La perpendiculaire en N à MN coupe MF en P, projection du centre de courbure C en M sur MF, et coupe MO en Q, point tel que QC soit perpendiculaire à l'axe focal : cela fournit deux constructions du centre de courbure, sauf aux sommets de l'axe focal où le rayon de courbure R = MC est égal à p = b2/a, paramètre de la conique (et longueur de la demi-corde issue de F et perpendiculaire à FF′). En un point quelconque, on a :

On retrouve aussi le paramètre comme longueur de la projection orthogonale de MN sur MF ou MF′. Si N′ est sur la médiatrice de FF′ et sur MN, MN′ se projette suivant une longueur égale à a sur MF ou MF′, et les trois vecteurs N′N, N′M et NM sont proportionnels aux nombres c2, a2 et a2 − c2 (b2 pour une ellipse, − b2 pour une hyperbole).
Les centres de courbure en les sommets A et B d'une ellipse sont alignés avec le point d'intersection des tangentes en A et B ; cette droite est perpendiculaire à AB ; la construction des cercles de courbure en A et B permet une construction graphique très soignée de l'arc AB.
Pôles et polaires
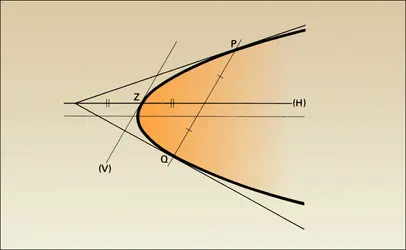
Si une corde MM′ coupe la directrice D en P, FP est une bissectrice de l'angle MFM′. Si MM′ passe par F, les tangentes en M et en M′ se coupent en T sur la directrice, et P est conjugué harmonique de F par rapport à M et M′ ; de plus l'angle MFT est droit. Cette directrice D est située à une distance a2/c de O, est perpendiculaire à l'axe focal et située du même côté de O que F. Elle n'existe pas pour un cercle pour lequel F, F′ et O sont confondus, d'où c = e = 0 ; cela fait que la définition monofocale, qui masque déjà le caractère de double symétrie de la conique, n'est pas aussi générale qu'elle paraît. Il existe naturellement une directrice analogue D′ pour l'autre foyer F′.
Pour une conique propre quelconque, à centre ou parabole, les conjugués harmoniques d'un point fixe M par rapport aux extrémités P et Q d'une corde passant par M sont situés sur une droite, appelée polaire de M. Ainsi une directrice est la polaire du foyer correspondant. Seul le centre n'a pas de polaire. Un point de la conique a sa tangente comme polaire. Toute droite ne passant pas par le centre éventuel est la polaire d'un certain point qui est appelé son pôle.
Si la polaire de M passe par M′, celle de M′ passe par M. Si M, P, Q sont alignés, leurs polaires sont concourantes et réciproquement. Si MT et MT′ sont des tangentes issues de M, la corde TT′ qui joint leurs points de contact est la polaire de M (cf. pour l'ellipse). Ces propriétés peuvent être obtenues très simplement par perspective (conique éventuellement) à partir des propriétés analogues pour le cercle, où elles sont bien connues ; elles sont projectives en dépit des apparences.
Diamètres
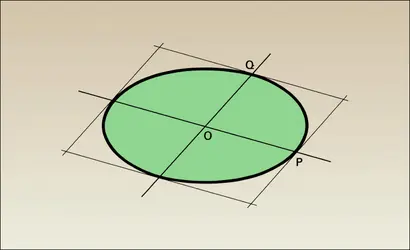
Donnons-nous une direction D ; les milieux des cordes parallèles à D sont situés sur un diamètre, c'est-à-dire une droite passant par le centre ( ellipse ou hyperbole) ou parallèle à l'axe (parabole). La conique est invariante dans la symétrie par rapport à ce diamètre parallèlement à la direction D. Fixons un point M ; à tout diamètre de direction D, associons son point d'intersection avec la perpendiculaire issue de M au diamètre conjugué de D défini ci-dessus. Ces points engendrent une hyperbole (équilatère), coupant la conique aux points où la normale passe par M, ce qui permet de les construire.
Pour une ellipse, à tout diamètre D, on peut associer le diamètre conjugué D′ dont D est à nouveau le conjugué. D et D′ coupent l'ellipse en P et Q, par exemple, tels que la tangente en P soit parallèle à D′, et forme avec D, D′ et la tangente en Q, un parallélogramme d' aire constante, égale à ab, comme on le voit en prenant les axes de l'ellipse pour D et D′. De plus OP2 + OQ2 = a2 + b2 est constant. De tels diamètres conjugués sont simplement les projections orthogonales de deux diamètres perpendiculaires d'un cercle de diamètre AA′ placé de façon que l'ellipse soit sa projection : la plupart des propriétés de la conjugaison (ainsi que la formule donnant l'aire de l'ellipse : S = πab) sont des conséquences immédiates de cette projection.
Accédez à l'intégralité de nos articles
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
Écrit par
- André WARUSFEL : universitaire
- Encyclopædia Universalis : services rédactionnels de l'Encyclopædia Universalis
Classification
Médias
Autres références
-
ESSAI POUR LES CONIQUES (B. Pascal)
- Écrit par Bernard PIRE
- 199 mots
- 1 média
Le premier écrit scientifique de Blaise Pascal (1623-1662) – Essai pour les coniques, composé avant qu'il ait atteint l'âge de dix-sept ans et publié à Paris en février 1640 – révèle aux savants de l'époque le génie précoce de son auteur. Adoptant la méthode proposée par Girard Desargues (1591-1661)...
-
APOLLONIOS DE PERGA (262 av. J.-C.?-? 190 av. J.-C.)
- Écrit par Jean MEYER
- 410 mots
Mathématicien grec de l'école d'Alexandrie, Apollonios de Perga est né probablement vingt-cinq ans après Archimède (donc vers ~ 262) et est mort sous le règne de Ptolémée IV (~ 222-~ 205). La renommée de son ouvrage principal, le Traité des sections coniques, lui valut le surnom...
-
ARCHIMÈDE (287-212 av. J.-C.)
- Écrit par Jean ITARD
- 2 724 mots
- 2 médias
...homogènes géométriquement définissables. Nous arrivons d'ailleurs ici à un tournant décisif. Nous ne connaissons encore que le mécanicien, l'ingénieur. Mais voilà qu'étudiant « la section du cône droit » – c'est ainsi qu'il appelait la parabole – il voit dans l'équation ... -
COURBES TRANSFORMATIONS DE
- Écrit par Robert FERRÉOL
- 5 623 mots
- 34 médias
Toute courbe peut être considérée comme une transformée de la plus simple d'entre elles, à savoir la droite, et les courbes sont donc toutes des transformées les unes des autres. Nous allons présenter dans cet article les plus classiques de ces transformations, en commençant par les plus simples. Cela...
-
DIOPHANTIENNES ÉQUATIONS
- Écrit par Jean-Louis COLLIOT-THÉLÈNE , Marcel DAVID et Encyclopædia Universalis
- 6 124 mots
- 1 média
La résolution en entiers de :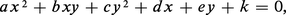
- Afficher les 12 références
Voir aussi