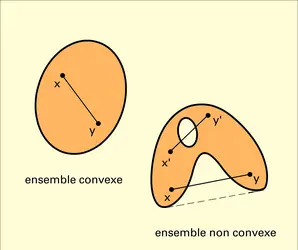
CONVEXITÉ Ensembles convexes

Intersections

Une partie des problèmes combinatoires est reliée à l'étude des intersections d'ensembles convexes qui sont toujours convexes, comme on l'a vu ci-dessus (l'ensemble vide est, par définition, convexe).

D'après un théorème démontré par Helly, l'intersection C d'une famille de convexes de Rⁿ, telle que l'intersection de toute sous-famille de (n + 1) de ces ensembles soit non vide, est non vide si l'une ou l'autre des hypothèses suivantes est réalisée : la famille est finie ou chacun des convexes de la famille est fermé et borné (c'est-à-dire compact). Ce théorème admet de nombreuses généralisations et applications.

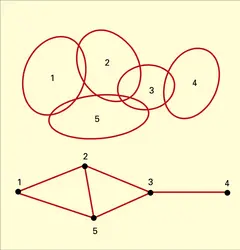
L'étude des propriétés des intersections d'ensembles convexes est facilitée par la notion de graphe d'intersection, qui est utilisée dans des domaines aussi variés que la génétique moléculaire, la psychologie et l'écologie. Pour toute famille d'ensembles, on appelle graphe d'intersection un graphe abstrait où chaque ensemble correspond à un sommet du graphe et où chaque intersection non vide est représentée par un arc réunissant les sommets correspondants ; la figure donne un exemple d'une famille d'ensembles convexes et de leur graphe d'intersection. Tout graphe ayant un nombre fini d'éléments est un graphe d'intersection d'ensembles convexes de R³, mais pas nécessairement un graphe d'intersection d'ensembles convexes de R² ou de R. Un graphe d'intervalles est un graphe d'intersection d'une famille finie d'ensembles convexes de R (ce sont des intervalles) ; on peut caractériser ces graphes d'intervalles, mais le problème correspondant pour le plan n'est pas résolu.

Étude des enveloppes convexes

Une autre série de problèmes combinatoires est la recherche de formes algébriques pour la représentation des enveloppes convexes. Voici, dans cet ordre d'idées, un théorème très simple et très utile, dû à Carathéodory : Si X est un sous-ensemble de Rⁿ et u un point de l' enveloppe convexe de X, alors u appartient à l'enveloppe convexe d'un sous-ensemble fini Y de X contenant au plus (n + 1) points. Par exemple, si X est un sous-ensemble du plan et si x appartient à l'enveloppe convexe de X, alors x appartient soit à X, soit à un segment ayant pour extrémités deux points de X, soit à un triangle ayant pour sommet trois points de X. Le théorème de Carathéodory a de nombreuses applications ; on en déduit, par exemple, que l'enveloppe convexe d'un ensemble fermé borné de Rⁿ est un ensemble fermé borné.

Polyèdres

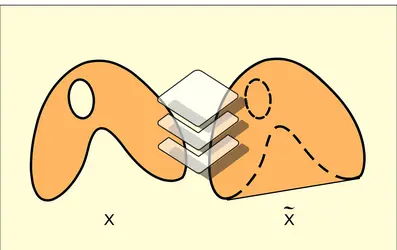
Parmi tous les problèmes combinatoires que l'on rencontre dans la théorie de la convexité, celui qui est le plus ancien et qui a été étudié de la manière la plus approfondie est la structure des faces des polyèdres convexes. Nous appellerons polyèdre tout sous-ensemble de Rⁿ intersection d'un nombre fini de demi-espaces fermés, en réservant la dénomination de polytope, aux polyèdres bornés ; un lemme, dû à Farkas, montre qu'un ensemble est un polytope si et seulement s'il est l'enveloppe convexe d'un nombre fini de points. On peut caractériser de même les cônes polyédraux comme enveloppes convexes d'un nombre fini de demi-droites de même origine. De manière générale, un sous-ensemble P de Rⁿ est un polyèdre si et seulement s'il satisfait à une des conditions équivalentes suivantes :

a) P est un ensemble convexe fermé qui a un nombre fini de faces ;

b) P est l'enveloppe d'un nombre fini de points et de demi-droites ;

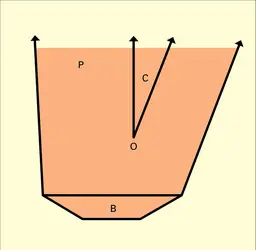
c) P est la somme vectorielle B + C d'un polytope B et d'un cône polyédral C, c'est-à-dire P est l'ensemble des points de la forme :

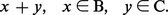
d) P est l'enveloppe convexe fermée de la réunion d'un polytope B et du translaté d'un cône polyédral. (On a représenté, sur la figure, un polyèdre P de dimension 2, ainsi que le polytope B et le cône C mentionnés ci-dessus.)

Le premier résultat, dans l'étude combinatoire des polytopes est le théorème d' Euler (1752), qui affirme que si v, e, f sont respectivement le nombre de sommets, d'arêtes et de faces d'un polytope de dimension 3, on a :

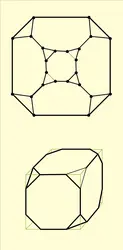
En 1934, Steinitz est parvenu à caractériser les graphes des polytopes de dimension 3 (on appelle graphe d'un polytope la structure combinatoire déterminée par les sommets et les arêtes) : le graphe d'un polytope de dimension 3 est équivalent à un graphe planaire (qui peut se dessiner dans le plan sans qu'il y ait aucune intersection d'arcs) connexe de degré 3 (c'est-à-dire qui ne peut être séparé en deux parties disjointes en enlevant moins de trois sommets). Par exemple, le graphe de la figure est le graphe du polytope obtenu en tronquant chacun des sommets d'un cube. On a découvert de nombreuses propriétés des graphes des polytopes de dimension n (par exemple, ils sont connexes de degré n), mais on ne connaît à ce jour aucune caractérisation combinatoire des graphes des polytopes de dimension > 3.

De nombreux problèmes de programmation linéaire et d' optimisation reviennent à trouver les points d'un polyèdre P où une fonction linéaire atteint son minimum ; on montre que, si P est borné, le minimum est alors atteint en un des sommets de P et certains procédés de résolution de programmes linéaires reposent sur cette propriété. On est donc amené à estimer le nombre de sommets d'un polytope P en fonction de sa dimension et du nombre de faces de dimension (n − 1). Pour 2 ≤ n < k, désignons par μ(n, k) le nombre maximum de sommets que possède un polyèdre de dimension n qui a k faces de dimension (n − 1) et par ϕ(n, k) la somme des coefficients binomiaux :