Abonnez-vous à Universalis pour 1 euro

DIOPHANTIENNES ÉQUATIONS

Article modifié le

Méthodes géométriques

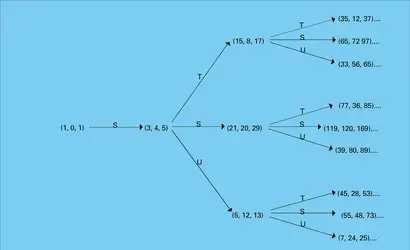
Pour classer les types d'équations, on utilise d'abord la dimension, ou nombre de variables indépendantes, du système proposé. Ainsi, en général, un système :

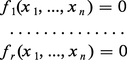
est de dimension (n − r). En dimension 1, on parle de courbes ; en dimension 2, de surfaces. Les solutions en nombres entiers ou rationnels du système proposé ne sont autres que les points entiers ou rationnels de la variété algébrique associée.

Déjà pour les courbes planes (une équation f (x, y) = 0), la classification par le degré s'avère trop grossière. Ainsi la théorie des cubiques planes à point double, comme :

avec a rationnel, est très simple, celle des cubiques planes sans point double, comme :
avec a et b rationnels non nuls et distincts, est beaucoup plus délicate. On est ainsi amené à utiliser des « invariants » de nature géométrique. Pour les courbes, on utilise le genre, nombre de trous de la surface de Riemann correspondante. Pour une courbe plane de degré d, à points multiples ordinaires, le genre vaut :
où la sommation s'étend à tous les points multiples, l'ordre de ceux-ci étant si.

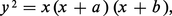
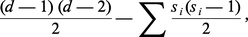
Courbes de genre zéro

On dispose ici d'une analyse complète. En ce qui concerne les points rationnels, la démarche est la suivante. Toute courbe de genre zéro peut, par un changement de variables, être ramenée à une conique plane (D.  Hilbert-A.  Hurwitz, 1891), soit ax2 + by2 + c = 0. D'après le théorème de Legendre (cf. supra), les conditions de congruence permettent de décider si cette conique a un point rationnel. S'il y a un point rationnel, soit M0, on peut les décrire tous, au moyen d'une paramétrisation biunivoque :

avec f et g des quotients de polynômes à coefficients rationnels (chaque point rationnel de la conique correspond à une unique valeur, rationnelle, du paramètre t). Une telle paramétrisation sera dite polynomiale. Pour obtenir cette paramétrisation, on fait simplement tourner une droite autour de M0 ; chaque droite de pente rationnelle t, passant par M0, recoupe la conique, qui est de degré 2, en un unique point, à coordonnées (x = f (t), y = g(t)) rationnelles. C'est ainsi qu'a été résolue plus haut l'équation de Pythagore.

Pour les points entiers sur une courbe de genre zéro, on dispose aussi d'une analyse complète (C. L. Siegel, 1929) : essentiellement, l'équation de Pell (cf. supra) est le seul cas non évident où il peut y avoir une infinité de points entiers.

Courbes de genre 1 : points rationnels

Ici, les conditions de congruence ne suffisent plus à assurer l'existence d'un point rationnel, comme le montre l'exemple 3 x3 + 4 y3 + 5 = 0 (E. S. Selmer, 1951). On dispose cependant d'un procédé remontant à Fermat (descente infinie) permettant d'étudier de telles courbes. C'est un problème ouvert de savoir si l'application systématique de ce procédé, conjointement avec les conditions de congruence, suffit toujours à déterminer la présence ou l'absence d'un point rationnel sur une courbe de genre 1.

Si l'on connaît un point rationnel sur une telle courbe, celle-ci peut être ramenée ( Poincaré, 1901) à une cubique plane non singulière :

avec P(x) un polynôme du troisième degré sans facteur multiple. On a là une courbe elliptique, objet fondamental tant en géométrie algébrique qu'en théorie des nombres. La géométrie algébrique montre qu'on ne peut pas ramener une telle courbe à une courbe de genre zéro. Il existe pourtant une paramétrisation des solutions complexes de (C), bien classique, mais, elle, de nature transcendante : la paramétrisation par les fonctions elliptiques (Weierstrass),. On voit sur cette paramétrisation que les solutions complexes de (C) peuvent être munies d'une structure de groupe abélien. En fait, la composition ainsi définie induit une composition des points rationnels de la cubique. Essentiellement, il s'agit de la construction suivante. Étant donné deux points rationnels de la cubique, la droite qui les joint, qui est à coefficients rationnels, recoupe la cubique en un troisième point, dont les coordonnées sont par force rationnelles : c'est le procédé de la corde pour engendrer de nouvelles solutions (on peut aussi utiliser la tangente en un point rationnel). On obtient ainsi une structure de groupe abélien sur l'ensemble des points rationnels de (C). L'important théorème de Mordell (1922), généralisé par Weil (1928), établi par descente infinie, dit que ce groupe appelé depuis groupe de Mordell-Weil, admet un nombre fini de générateurs. En d'autres termes, étant donné une cubique (C), il existe un nombre fini de points rationnels situés dessus tels que tous les autres points rationnels de (C) puissent être obtenus à partir de ceux-ci par itération du procédé de la corde et de la tangente. Étant donné une courbe (C), on sait borner le nombre minimal de générateurs du groupe de Mordell-Weil associé (rang), mais on n'a pas de méthode générale pour déterminer le rang, a fortiori pour construire explicitement un système de générateurs. On dispose seulement d'un algorithme conditionnel (Yu. I. Manin, 1973), reposant sur deux conjectures. L'une, de Weil, relie les courbes elliptiques aux formes modulaires. L'autre, de B. Birch et H. P. F. Swinnerton-Dyer (1965), affirme que le rang d'une courbe elliptique est donné par l'ordre du zéro au point complexe z = 1 d'une certaine fonction méromorphe dont la définition fait intervenir le nombre de solutions modulo p, nombre premier, de l'équation (C), cela pour tous les nombres premiers p (cf. fonction zeta). L'ordinateur a donné un grand poids à cette conjecture, et des progrès théoriques ont été effectués.

Courbes de genre au moins égal à 2 : points rationnels

Parmi les courbes de genre au moins égal à 2, on trouve les courbes planes non singulières de degré au moins 4. Là encore, on ne peut ramener l'étude de telles courbes à l'étude de celles de genre inférieur ou égal à 1. On ne dispose d'aucun procédé permettant d'engendrer un nombre infini de solutions à partir d'un nombre fini d'entre elles. Mordell a ainsi conjecturé (1922) qu'une telle équation n'admettrait jamais qu'un nombre fini de solutions rationnelles. Cette conjecture a été démontrée par G. Faltings en juin 1983.

Points entiers sur les courbes de genre au moins 1

On dispose du théorème général de C. L.  Siegel (1929) selon lequel une telle courbe n'a qu'un nombre fini de points entiers. La démonstration utilise d'une part le théorème de A. Weil (1928), étendant celui de Mordell, d'autre part la mauvaise approximation par des rationnels des irrationnels algébriques. Ce résultat englobe celui de Thue (1909), lui aussi fondé sur les approximations diophantiennes : l'équation

où f est un polynôme homogène irréductible à coefficients entiers de degré au moins égal à 3, et m est un entier non nul, ne possède qu'un nombre fini de solutions entières.

Dans beaucoup de cas, en particulier pour les équations y2 = P(x) où le polynôme P a au moins trois zéros distincts, A. Baker a donné des majorations effectives (mais grandes) pour la taille possible des solutions entières ; ainsi, pour l'équation de Thue ci-dessus :

où d est le degré de f, et H un entier dépendant de la taille de m et des coefficients de f. Dans certains cas particuliers, ces méthodes permettent même de trouver toutes les solutions entières.

Surfaces rationnelles

Les surfaces rationnelles sont les analogues en dimension 2 des courbes unicursales, celles qui peuvent être paramétrées de façon polynomiale si l'on autorise les coefficients des polynômes définissant le paramétrage à être des nombres complexes. Parmi celle-ci, on trouve les surfaces non singulières de l'espace ordinaire définies par une équation de degré 2 ( quadriques) ou 3 (surfaces cubiques), mais aussi des équations de degré supérieur, comme :

avec a(x) et b(x) des polynômes non nuls de degré quelconque.

On est loin de disposer ici de résultats aussi satisfaisants que pour les courbes de genre zéro. Dans certains cas : quadriques (Hasse-Minkowski, cf. supra), surfaces cubiques

avec ab = cd ≠ 0 (E. S. Selmer, 1953), les conditions de congruence (et la condition réelle) suffisent à assurer l'existence de points rationnels. Cela ne vaut pas en général, comme le montre l'exemple (J. W. S. Cassels-M. J.T. Guy, 1966) :

Abonnez-vous à Universalis pour 1 euro

Si une quadrique a un point rationnel, on peut encore donner une paramétrisation polynomiale essentiellement biunivoque des points rationnels, en utilisant la même méthode que pour les coniques.

Une telle paramétrisation est encore possible pour une surface cubique de l'espace ordinaire, soit Σ, qui contient deux droites D et D′ définies par des équations à coefficients rationnels, et ne se coupant pas. Choisissons un plan π, d'équation ax + by + cz + d = 0, avec a, b, c, d rationnels. Pour M un point rationnel du plan π, la droite DM, intersection des deux plans engendrés l'un par (M, D), l'autre par (M, D′), est définie par des équations à coefficients rationnels. Elle coupe la surface cubique Σ en trois points : celui qui est situé sur D et celui qui est situé sur D' sont définis par des équations à coefficients rationnels, le troisième, soit f (M), est donc à coordonnées rationnelles. On vérifie que la correspondance qui à M associe f (M) définit une paramétrisation polynomiale essentiellement biunivoque des points rationnels de Σ par ceux de π. C'est ainsi qu'on trouve la solution générale due à Euler de l'équation : x3 + y3 + z3 = 1

Des méthodes fines de géométrie algébrique montrent qu'une telle paramétrisation polynomiale biunivoque à coefficients rationnels est souvent impossible, ainsi pour :

où a est un rationnel qui n'est pas un cube (Yu. I. Manin, 1970). On peut cependant, pour une surface cubique non singulière qui possède au moins un point rationnel, trouver des familles polynomiales à deux vrais paramètres (c'est-à-dire qu'on ne peut réduire à un seul paramètre), soit :
avec A,B,C quotients de polynômes en u et y à coefficients rationnels, mais en général même un nombre fini de telles familles ne suffit pas à décrire tous les points rationnels de la surface cubique. On obtient néanmoins beaucoup de solutions rationnelles. En spécialisant les paramètres, on obtient par exemple que tout rationnel est somme de trois cubes de rationnels :
(Ryley, 1825 ; H. W. Richmond, 1930).

Abonnez-vous à Universalis pour 1 euro

En s'inspirant de la méthode de Mordell-Weil, F. Châtelet (1959) a montré qu'un nombre fini de solutions paramétriques polynomiales (à 4 variables) permet de décrire toutes les solutions rationnelles de :

avec a, b, c rationnels non nuls. On ignore par contre si une solution polynomiale, même partielle, à deux vrais paramètres et à coefficients rationnels est possible pour l'équation générale :
où a(x) et b(x) sont des polynômes non nuls.

Pour les points entiers des surfaces cubiques, on a des résultats épars. Soit par exemple l'équation :

avec n entier fixé, à résoudre en (x, y, z) entiers. On voit facilement (congruences modulo 9) qu'il n'y a pas de solutions si n est congru à ± 4 modulo 9. Sinon, on ne sait pas s'il y a toujours une solution, par exemple pour n = 30, et, s'il y en a une, s'il y en a une infinité. L'identité :
donne une infinité de solutions pour n = 2, mais, pour n = 3, on ne connaît que les solutions (1, 1, 1) et (4, 4, − 5).

Pour :

avec a et b entiers, on dispose d'un processus (Markov, Hurwitz) permettant d'engendrer toutes les solutions entières à partir d'un nombre fini, explicitement calculables, d'entre elles.

Abonnez-vous à Universalis pour 1 euro

On conjecture (P. Erdös, E. G. Straus) que l'équation :

avec n entier fixé, n > 1, à résoudre en entiers positifs x, y, z, a toujours des solutions (c'est un cas particulier du problème des fractions égyptiennes, où l'on cherche à écrire un rationnel comme somme d'un nombre donné d'inverses d'entiers). Cette conjecture a été établie pour n ≤ 108.

Surfaces analogues aux courbes de genre 1

L'analogue immédiat, du point de vue de la géométrie algébrique, consiste en les surfaces abéliennes (pour lesquelles il est difficile de donner des équations !). Le théorème de A.  Weil (1928) nous renseigne sur les points rationnels, mais on ignore s'il n'y a qu'un nombre fini de points entiers.

Un autre analogue consiste en les surfaces non singulières de l'espace ordinaire, de degré 4. Une conjecture d' Euler affirme que l'équation :

n'a pas d'autres solutions rationnelles que (± 1, 0, 0), (0, ± 1, 0) et (0, 0, ± 1), mais on sait seulement qu'une autre solution devrait avoir un dénominateur au moins égal à 220 000. Euler donna une infinité de solutions rationnelles de :
au moyen d'une solution à un paramètre ; par exemple :
La géométrie algébrique montre qu'aucune solution, même partielle, polynomiale à deux vrais paramètres n'est possible. Cependant, en utilisant le fait que la surface ci-dessus peut être fibrée en courbes elliptiques, on peut donner une infinité de solutions essentiellement distinctes à un paramètre (H. P. F. Swinnerton-Dyer, 1971).

Surfaces analogues aux courbes de genre au moins 2

Parmi celles-ci, on trouve les surfaces non singulières d'équation :

avec f de degré au moins 5. Une fois de plus, elles ne peuvent être ramenées aux surfaces précédentes. Il peut exister des solutions à un paramètre, mais une conjecture analogue à celle de Mordell pour les courbes de genre au moins 2 voudrait que, pour une telle surface, les points rationnels soient concentrés sur un nombre fini de courbes algébriques tracées sur la surface.

Accédez à l'intégralité de nos articles

  • Des contenus variés, complets et fiables
  • Accessible sur tous les écrans
  • Pas de publicité

Découvrez nos offres

Déjà abonné ? Se connecter

Écrit par

  • : chargé de recherche au C.N.R.S.
  • : professeur à la faculté des sciences de Reims
  • Encyclopædia Universalis : services rédactionnels de l'Encyclopædia Universalis

Carte mentale
Élargissez votre recherche dans Universalis

Classification

Média

Équation de Pythagore - crédits : Encyclopædia Universalis France

Équation de Pythagore

Encyclopædia Universalis France

Autres références

  • PRIX ABEL 2020

    • Écrit par
    • 1 824 mots
    • 2 médias
    Hillel Furstenberg - crédits : Yosef Adest/ Hebrew University of Jerusalem

    Le prix Abel 2020 a été attribué conjointement à Hillel Furstenberg et Gregory Margulis « pour l'utilisation visionnaire de méthodes issues de la théorie des probabilités et de celles des systèmes dynamiques en théorie des groupes, théorie des nombres et combinatoire ».

    Hillel...

  • ARITHMÉTIQUES (Diophante)

    • Écrit par
    • 189 mots

    Diophante d'Alexandrie, parfois appelé le « père de l'algèbre », est connu par son ouvrage les Arithmétiques, qui traite des solutions des équations algébriques. On ne sait pratiquement rien de sa vie et ses dates de naissance et de mort sont très controversées. Les Arithmétiques...

  • BAKER ALAN (1939-2018)

    • Écrit par
    • 338 mots

    Alan Baker, mathématicien britannique, lauréat de la médaille Fields en 1970 pour ses travaux en théorie des nombres, est né le 19 août 1939 à Londres. Il a fait ses études supérieures à l'University College de Londres puis au Trinity College de Cambridge où il soutient sa thèse de doctorat en...

  • CASSELS JOHN WILLIAM SCOTT (1922-2015)

    • Écrit par
    • 328 mots

    Mathématicien britannique, spécialiste de la théorie des nombres. Né le 11 juillet 1922 à Durham, John William Scott Cassels est le fils du directeur de l'agriculture du comté de Durham dans le nord de l'Angleterre. Après des études secondaires et supérieures à Édimbourg (Écosse), il est admis en...

  • Afficher les 16 références

Voir aussi

Abonnez-vous à Universalis pour 1 euro

Rejoignez-nous

Inscrivez-vous à notre newsletter