Abonnez-vous à Universalis pour 1 euro

NORMÉS ESPACES VECTORIELS

Article modifié le

L'analyse fonctionnelle linéaire, en tant que théorie générale, s'est créée au début du xxe siècle, autour des problèmes posés par les équations intégrales. Entre 1904 et 1906, D. Hilbert (1862-1943) est amené à étudier des développements en séries de fonctions orthogonales, ainsi que des formes quadratiques à une infinité de variables. À sa suite, F. Riesz (1880-1956) et E. Fischer (1875-1959) étudient les fonctions de carré intégrable et la convergence en moyenne quadratique, puis F. Riesz introduit les espaces Lp pour 1 < p < + ∞ et la moyenne d'ordre p. Toutefois, ce n'est que vers 1920 que la notion d'espace normé abstrait est dégagée, principalement par S.  Banach (1892-1945), et ce n'est qu'en 1929-1930 que J. von Neumann (1903-1957) propose une présentation axiomatique des espaces de Hilbert. S. Banach, dans sa thèse de 1920 intitulée : Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales, écrit : « L'ouvrage présent a pour but d'établir quelques théorèmes valables pour différents champs fonctionnels, que je spécifie dans la suite. Toutefois, afin de ne pas être obligé à les démontrer isolément pour chaque champ particulier, ce qui serait bien pénible, j'ai choisi une voie différente que voici : je considère d'une façon générale les ensembles d'éléments dont je postule certaines propriétés, j'en déduis des théorèmes et je démontre ensuite de chaque champ fonctionnel particulier que les postulats adoptés sont vrais pour lui. »

Par la suite, les espaces vectoriels normés ont été étudiés de manière autonome, notamment du point de vue de leur géométrie. Parallèlement, l'obligation, en théorie des équations aux dérivées partielles par exemple, de considérer des espaces de fonctions dont la topologie n'est pas déduite d'une norme a motivé l'introduction d'une structure plus générale : celle d' espace vectoriel topologique. Toutefois, en raison de la spécificité des problèmes et des méthodes, les espaces vectoriels normés ne doivent pas être considérés comme de simples cas particuliers d'espaces vectoriels topologiques. De plus, les espaces vectoriels topologiques les plus importants peuvent être construits en un certain sens à l'aide d'espaces vectoriels normés, et bénéficient donc pour leur étude des propriétés de ces derniers. En retour, les espaces vectoriels topologiques interviennent dans l'étude des espaces normés, notamment pour tout ce qui concerne les convergences faibles.

Abonnez-vous à Universalis pour 1 euro

Dans la seconde moitié du xxe siècle, l'évolution de la théorie est considérable, particulièrement en ce qui concerne la géométrie des espaces de Banach et ses liens avec les ensembles d'opérateurs que l'on peut définir entre les espaces étudiés.

Espaces vectoriels normés, espaces de Banach : définitions et premières propriétés

Dans ce qui suit, on ne considérera que des espaces vectoriels sur le corps R des nombres réels ou sur le corps C des nombres complexes. Pour éviter de préciser à chaque fois, on désignera par K ce corps de base ; pour α ∈ K, la notation |α| désignera donc soit la valeur absolue de α si K = R, soit le module de α si K = C.

Soit E un espace vectoriel sur K. On appelle norme sur E une application (notée traditionnellement x ↦ ∥x∥ ; on dit aussi que ∥x∥ est la norme de x) de E dans l'ensemble R+ des nombres réels positifs ou nuls qui possède les propriétés suivantes :

Abonnez-vous à Universalis pour 1 euro

(1) Condition de séparation :

(2) Homogénéité :

quels que soient x ∈ E et λ ∈ K ;

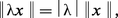
(3) Inégalité du triangle :

quels que soient x, y ∈ E.

Abonnez-vous à Universalis pour 1 euro

Un espace vectoriel muni d'une norme s'appelle un espace vectoriel normé. Remarquons que la restriction d'une norme à un sous-espace vectoriel est une norme, appelée norme induite, sur ce sous-espace. Si la condition de séparation n'est pas satisfaite, on dit qu'on a seulement une semi-norme ; l'espace quotient de E par la relation d'équivalence :

est alors muni de manière naturelle d'une norme, car le nombre ∥x∥ ne dépend que de la classe de x (espace normé associé).

Tout espace vectoriel E est un espace métrique pour la distance :

déduite de la norme. On peut donc appliquer aux espaces vectoriels normés le langage géométrique de l'analyse (boules, ouverts et fermés, convergence, etc.) introduit dans l'article espaces métriques. Remarquons que si d est une distance sur un espace vectoriel déduite d'une norme, elle possède la propriété suivante d'invariance par translation :
quels que soient x, y, z ∈ E. Ainsi, les boules de centre z sont les translatées des boules centrées à l'origine 0 de l'espace vectoriel qui s'obtiennent toutes par homothétie (d'après l'homogénéité de la norme) à partir de la boule unité ouverte :
ou de la boule unité fermée :

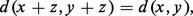
Ces boules unités sont des ensembles convexes, et on peut reconstituer la norme à partir de la boule unité par exemple ; on suppose ici, bien entendu, K = R (cf. convexité, chap. 4).

Abonnez-vous à Universalis pour 1 euro

On dit qu'un espace vectoriel normé E est complet, ou encore est un espace de Banach, s'il est complet pour la métrique déduite de sa norme. Cela signifie ici qu'une suite (xn) d'éléments de E est convergente si et seulement si :

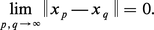
Si E est un espace vectoriel normé, on montre facilement que son complété (au sens de la théorie des espaces métriques ; cf. espaces métriques, chap. 3) peut être muni d'une structure d'espace de Banach qui prolonge celle de E. Ainsi, tout espace vectoriel normé peut être plongé dans un espace de Banach dont il soit un sous-espace dense ; ce complété est unique à un isomorphisme d'espace vectoriel normé près.

Il faut enfin mentionner que les espaces vectoriels normés apparaissent comme le cadre naturel de la théorie des séries et des familles sommables.

Abonnez-vous à Universalis pour 1 euro

Les exemples que nous donnons maintenant fournissent un premier catalogue des espaces normés les plus courants. Remarquons que lorsque ces espaces ne sont pas complets, en vertu de ce qui a été dit précédemment, on étudie leur complété afin de se ramener à un espace de Banach.

Espaces de dimension finie

Bien entendu, l'application x ↦ |x| est une norme sur K considéré comme un espace vectoriel de dimension 1 sur lui-même (et aussi d'ailleurs de C comme espace vectoriel de dimension 2 sur R).

Plus généralement, soit E un espace de dimension finie n que l'on identifie à Kn par le choix d'une base. On considère usuellement les normes :

pour x = (x1, x2, ..., xn) ∈ Kn ; en fait, pour tout nombre réel positif p > 0,
est une norme sur Kn (espaces de Minkowski). Sur un espace de dimension finie, on montre que toutes les normes sont équivalentes (cf. définition précise in chap. 3) ; cette propriété, comme on le verra ci-dessous, est caractéristique des espaces de dimension finie, et la situation est fondamentalement différente dans ceux de dimension infinie. Les espaces de dimension finie sont aussi caractérisés par le fait que leur boule unité est compacte (théorème de Riesz). Mentionnons enfin que tout espace vectoriel normé de dimension finie est nécessairement complet.

Abonnez-vous à Universalis pour 1 euro

La norme ∥.∥2 sur Cn est associée au produit scalaire hermitien :

qui munit Cn d'une structure hilbertienne ; de manière générale, tout espace préhilbertien E est un espace vectoriel normé si on le munit de la norme :
en désignant par (x|y) le produit hermitien de x et y (cf. espace de hilbert).

Norme de la convergence uniforme

Si X est un ensemble, désignons par E = B(X, K) l'espace vectoriel des applications bornées de X dans K (rappelons que l'on a toujours K = R ou C) ; on appelle norme de la convergence uniforme la norme sur E définie par :

On montre que B(X, K), muni de la norme de la convergence uniforme est un espace complet. Dire qu'une suite (f n) de fonctions converge vers f pour cette norme signifie ici que :

c'est-à-dire que la suite des fonctions f n converge uniformément vers f. Dans le cas où X est un espace topologique, on montre que le sous-espace C∞(X, K) des applications continues bornées de X dans K est fermé dans B(X, K) et, par suite (cf. espaces métriques, chap. 3), est aussi un espace de Banach pour la norme de la convergence uniforme.

Espaces liés à l'intégration

Soit[a, b]un intervalle fermé borné de R ; désignons par C([a, b], K) l'espace vectoriel des fonctions continues définies sur[a, b]à valeurs dans K ; pour tout nombre réel p ≥ 1, on peut considérer la norme :

  appelée norme de la convergence en moyenne d'ordre p. Ces normes sont deux à deux non équivalentes, et C([a, b], K) n'est complet pour aucune d'entre elles (alors que C([a, b], K) est complet pour la norme de la convergence uniforme). Le complété de C([a, b], K) pour une telle norme (cf. espaces métriques, chap. 3) n'est autre que l'espace Lp ([a, b], K) des classes de fonctions à valeurs dans K, de puissance p-ième intégrale sur[a, b]pour la mesure de Lebesgue (cf. intégration et mesure, chap. 4). Pour p = 2 on obtient un espace de Hilbert, la norme étant associée au produit scalaire :

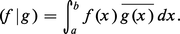
Rappelons qu'une fonction mesurable définie sur[a, b]à valeurs dans K (cf. intégration et mesure, chap. 3) est dite essentiellement bornée par M si la mesure de l'ensemble des x tels que |f (x)| > M est nulle ; la borne supérieure essentielle, notée ∥f ∥∞, est le plus petit M réalisant la condition précédente.

Abonnez-vous à Universalis pour 1 euro

L'espace L∞ ([a, b], K) des classes de fonctions essentiellement bornées sur[a, b]à valeurs dans K est normé par ∥f ∥∞ ; c'est alors un espace de Banach.

Il existe d'autres exemples intéressants d'espaces de Banach liés à l'intégration, notamment les espaces d'Orlicz (cf. convexité-Fonctions convexes).

Espaces de suites

Sur l'espace l∞ des suites bornées d'éléments de K on peut définir la norme :

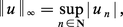
où u est la suite de terme général un ; on obtient ainsi un espace de Banach. Remarquons que cet exemple peut être considéré comme un cas particulier de norme de convergence uniforme sur un espace B(X, K) de fonctions bornées en prenant X = N.

L'espace c0 des suites d'éléments de K qui convergent vers 0 (et sont donc bornées), muni de la norme induite par la norme ∥ ∥∞ de l∞, est un espace de Banach ; c'est un sous-espace fermé de l∞. On dispose d'un résultat analogue pour l'espace c des suites convergentes d'éléments de K.

Abonnez-vous à Universalis pour 1 euro

Pour p ≥ 1 on définit l'espace lp des suites u = (un)n ≥ 0 d'éléments de K telles que ∞ |un|p < + ∞ ; muni de la norme : n = 0

lp est un espace de Banach. Dans le cas p = 2, on obtient un espace de Hilbert, la norme étant déduite du produit scalaire

Dans toute la suite, les espaces l∞,c,c0, lp, Lp ([a, b], K) seront considérés comme normés de la façon indiquée dans les exemples. D'autre part, du point de vue des notations, lorsque aucune confusion n'en résulte, on se permettra de noter C(X), Lp ([a, b]) les espaces C(X,K), Lp ([a, b], K).

Continuité d'une application linéaire

Soit E et F des espaces vectoriels normés sur K (égal à R ou C) et :

une application linéaire, c'est-à-dire telle que :
quels que soient x, y ∈ E et λ, μ ∈ K. Les trois conditions suivantes, apparemment de plus en plus fortes, sont en fait équivalentes :

(1) L'application u est continue au point 0 ∈ E ;

(2) L'application u est continue partout ; (3) Il existe une constante M telle que :

pour tout x ∈ E (on exprime cette condition en disant que u est borné).

Ainsi, la continuité en un seul point (on se ramène à l'origine par translation) entraîne que u est uniformément continue (et même lipschitzienne, cf. espaces métriques, chap. 2), car on a (la linéarité est bien entendu ici essentielle) : u(x) − u(y) = u(x − y), d'où :

Abonnez-vous à Universalis pour 1 euro

Cette importante propriété rend les applications linéaires continues redevables des résultats relatifs aux applications uniformément continues. Le théorème de prolongement (cf. espaces métriques, chap. 3) donne ici : soit E un espace vectoriel normé, E′ un sous-espace dense et u : E′ → F une application linéaire continue de E′ dans un espace de Banach F ; alors il existe un prolongement linéaire continu unique ũ : E → F à l'espace E tout entier (la linéarité du prolongement est évidente par continuité).

Comparaison de normes

Considérons deux normes ∥.∥1 et ∥.∥2 sur un même espace vectoriel E et désignons par E1 et E2 les espaces vectoriels normés correspondants. On dit que la norme ∥.∥1 est plus fine que la norme ∥.∥2 si l'application identique de E1 dans E2 est continue, ce qui signifie que tout ouvert pour la norme ∥.∥2 est un ouvert pour la norme ∥.∥1.

La condition ci-dessus montre que cela équivaut à dire qu'il existe une constante a > 0 telle que :

pour tout x ∈ E. On dit que les deux normes sont équivalentes si elles définissent les mêmes ouverts, c'est-à-dire s'il existe des constantes strictement positives a et b telles que :

Abonnez-vous à Universalis pour 1 euro

Par exemple, si E et F sont des espaces vectoriels normés de normes respectives ∥.∥ et ∥.∥′, on obtient sur E × F trois normes équivalentes en prenant pour norme de l'élément (x, y) ∈ E × F respectivement l'un des trois nombres :

On montre que, sur un espace vectoriel de dimension finie, toutes les normes sont équivalentes, mais inversement ce n'est plus nécessairement le cas en dimension infinie, comme le démontre l'exemple de l'espace E = C([0, 1]) muni des normes :

on a ici ∥f ∥1 ≤ ∥f ∥∞, et, par suite, la norme de la convergence uniforme est plus fine que la norme de la convergence en moyenne, mais ces deux normes ne sont pas équivalentes. Il suffit pour s'en convaincre de remarquer que la suite (f n) d'éléments de E, définie par :
converge en moyenne vers la fonction 0 mais ne converge pas uniformément, car ∥f n∥1 = 1/(2 n) et ∥f n∥∞ = 1.

Norme d'une application linéaire

Si E et F sont des espaces vectoriels normés, on désigne par Lc(E, F) l'espace vectoriel des applications linéaires continues de E dans F. La présence du c en indice est destinée à éviter la confusion avec l'ensemble de toutes les applications linéaires (continues ou pas) de E dans F que les algébristes notent (cf. algèbre linéaire et multilinéaire) L(E, F) ; dans la pratique, cet indice saute, car le contexte indique toujours assez clairement si on impose la continuité ou pas... Dans ce qui suit, nous ne considérerons que des applications linéaires continues et, le lecteur (éventuel) étant prévenu, nous désignerons par L(E, F) l'espace vectoriel des applications linéaires continues de E dans F.

On vérifie que l'application :

est une norme sur l'espace vectoriel L(E, F). Le nombre ∥u∥ s'appelle la norme de l'application linéaire u et admet aussi les expressions :
ainsi, c'est la plus petite constante M telle que l'on ait :
pour tout x ∈ E.

Abonnez-vous à Universalis pour 1 euro

On montre que l'espace vectoriel normé L(E, F) est complet si et seulement si F est complet. En particulier, le dual topologique L(E, K), qui est l'espace vectoriel des formes linéaires continues sur E, est toujours un espace de Banach ; on le note E* (ne pas confondre avec le dual algébrique).

Remarquons enfin que si E, F et G sont trois espaces vectoriels normés, si u : E → F et v : F → G sont des applications linéaires continues, alors on a :

en particulier, l'algèbreL(E, E) = L(E) des endomorphismes d'un espace vectoriel normé est une algèbre normée pour la norme introduite ci-dessus (cf. algèbres normées).

Hyperplans fermés

Soit E un espace vectoriel normé et F un sous-espace vectoriel de E. Si x et y appartiennent à l'adhérence F− de F dans E, cela signifie qu'il existe des suites (xn) et (yn) d'éléments de F qui convergent respectivement vers x et y ; pour λ, μ ∈ K, la suite (λxn + μyn) d'éléments de F converge vers λx + μy qui appartient donc aussi à F−. Ainsi, l'adhérence d'un sous-espace vectoriel est un sous-espace vectoriel. Si F est un sous-espace de dimension finie de E, on montre qu'il est toujours fermé, mais, dans les espaces de dimension infinie, il peut exister des sous-espaces distincts de leur adhérence, comme on va le voir.

Rappelons (cf. algèbre linéaire et multilinéaire, chap. 4) qu'on appelle hyperplan d'un espace vectoriel tout sous-espace strict maximal, c'est-à-dire de codimension 1 ; si H est un hyperplan de E, il existe une forme linéaire u : E → K, unique à un scalaire près, telle que H soit le noyau de u (on dit que u(x) = 0 est l'équation de l'hyperplan). Supposons E normé et soit H un hyperplan ; l'adhérence H̄ est un sous-espace vectoriel de E qui contient H, et par suite, d'après la maximalité de H, on a soit H = H̄, c'est-à-dire que l'hyperplan H est fermé, soit H̄ = E, c'est-à-dire que l'hyperplan est dense dans E. On montre facilement que, avec les notations données ci-dessus, l'hyperplan H est fermé si et seulement si la forme linéaire u est continue.

Abonnez-vous à Universalis pour 1 euro

La notion d'hyperplan partout dense étant peu intuitive, donnons un exemple simple de cette situation. Soit E l'espace vectoriel des polynômes à coefficients réels, muni de la norme de la convergence uniforme sur [0, 1], c'est-à-dire :

la forme linéaire u définie par :
n'est pas continue, car la suite (Pn), définie par Pn(t ) = (t/2)n, converge vers 0 dans E ; en effet, ∥Pn∥ = (1/2)n), alors que u(Pn) = 1 ne converge pas vers 0. Il en résulte que l'espace vectoriel des polynômes P qui admettent le nombre 2 pour racine forme un hyperplan partout dense de E.

Isomorphismes, isométries

Une application linéaire bijective u d'un espace normé E sur un espace normé F telle que u et u-1 soient continues est un isomorphisme de E sur F ; deux espaces normés E et F sont isomorphes s'il existe un isomorphisme de E sur F ; du point de vue topologique, les espaces E et F sont homéomorphes (cf. topologie-Topologie générale). Compte tenu de ce qui a été dit sur la continuité des applications linéaires, pour qu'une application linéaire surjective de E sur F soit un isomorphisme il faut et il suffit qu'il existe deux constantes C1 > 0 et C2 > 0 telles que pour tout élément x de E :

(Remarquons que l'injectivité est conséquence de l'inégalité C1∥x∥E ≤ ∥u(x)∥F et de la linéarité de u, si bien que si u n'est pas surjective on peut tout de même dire que u est un isomorphisme de E sur u(E).)

Abonnez-vous à Universalis pour 1 euro

Une application linéaire bijective u d'un espace normé E sur un espace normé F telle que pour tout x de E ∥u(x)∥F = ∥x∥E est une isométrie, ou encore un normisomorphisme de E sur F ; s'il existe une isométrie de E sur F, les espaces E et F sont dits isométriques ou encore normisomorphes.

Tous les espaces de Banach de même dimension finie n sur K sont isomorphes ; en revanche, ils ne sont pas tous isométriques comme le montre la considération des normes ∥ ∥2 et ∥ ∥∞ par exemple. Si 1 ≤ p < q < + ∞, aucun sous-espace fermé de dimension infinie de lp n'est isomorphe à un sous-espace de lq ; aucun sous-espace fermé de c0 n'est isomorphe à un sous-espace de lp. K1 et K2 étant deux espaces compacts, C (K1, R) et C (K2, R) sont isométriques si et seulement si K1 et K2 sont homéomorphes ; C ([0,1], R) et C ([0,1] × [0,1], R) ne sont donc pas isométriques ; on peut montrer cependant qu'ils sont isomorphes.

Accédez à l'intégralité de nos articles

  • Des contenus variés, complets et fiables
  • Accessible sur tous les écrans
  • Pas de publicité

Découvrez nos offres

Déjà abonné ? Se connecter

Écrit par

  • : maître assistant à la faculté des sciences de Marseille-Luminy
  • : maître de conférences honoraire à l'université de Paris-VII

Carte mentale
Élargissez votre recherche dans Universalis

Classification

Autres références

  • ALGÈBRE

    • Écrit par
    • 7 145 mots
    Unespace vectoriel normé sur le corps K des nombres réels ou des nombres complexes est un espace vectoriel E sur lequel est définie une fonction x → ∥x∥, à valeurs réelles positives, possédant les propriétés suivantes, qui généralisent celle de la longueur d'un vecteur dans les espaces...

  • BANACH STEFAN (1892-1945)

    • Écrit par
    • 1 599 mots
    Le nom de Banach restera lié auxespaces vectoriels normés complets, appelés par lui espaces du type (B) et universellement dénommés de nos jours «  espaces de Banach » (terminologie introduite par M. Fréchet en 1928). La notion d'espace normé général apparaît pour la première fois dans les travaux...

  • CONVEXITÉ - Ensembles convexes

    • Écrit par
    • 4 668 mots
    • 7 médias
    Enveloppe convexe - crédits : Encyclopædia Universalis France
    La convexité intervient de manière essentielle dans les espaces vectoriels de l'analyse :espaces vectoriels normés, ou plus généralement espaces vectoriels topologiques localement convexes, c'est-à-dire où tout point a un système fondamental de voisinages convexes ; on se limitera ici à de rapides...

  • HILBERT ESPACE DE

    • Écrit par et
    • 3 232 mots
    La semi-norme précédente est une norme si et seulement si l'espace vectoriel E est hermitien. Le nombre réel positif ∥x∥ s'appelle alors norme hermitienne du vecteur x, et le nombre ∥x − y∥ distance hermitienne des points x et y. Un vecteur de norme 1 est dit unitaire. Dans...

Voir aussi

Abonnez-vous à Universalis pour 1 euro

Rejoignez-nous

Inscrivez-vous à notre newsletter