GAMMA FONCTION

Introduites pour la première fois comme nouvelles transcendantes par L. Euler, la fonction gamma et la fonction bêta, qui s'y ramène, sont les plus importantes « fonctions spéciales » étudiées, au fur et à mesure des besoins, depuis le xviii^e siècle. C'est ainsi que la fonction gamma intervient dans de nombreuses estimations asymptotiques des « grands nombres », en statistique notamment ; elle intervient aussi dans la théorie des séries de Dirichlet (cf. théorie des nombres-Théorie analytique des nombres, fonction zêta).

Nous avons choisi ici d'aborder la fonction gamma dans le domaine réel. Appliquant le principe du prolongement analytique (cf. fonctions analytiques – Fonctions analytiques d'une variable complexe, chap. 1), on obtient ensuite l'extension au champ complexe de la plupart des formules.

La fonction gamma dans le domaine réel

Une intégration par parties montre facilement que, pour tout entier positif n, on a :

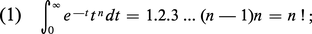
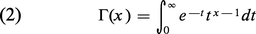
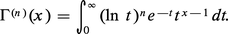
Remarquons qu'avec la définition (2) on a, en tenant compte de (1) :

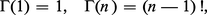
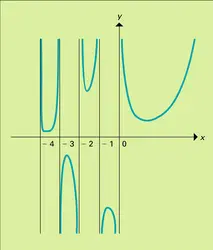
Relation fonctionnelle et graphe

Remplaçant x par x + 1 dans (2) et intégrant par parties, on obtient :

ce qui donne, en faisant tendre a vers 0 et A vers l'infini, la relation fonctionnelle :

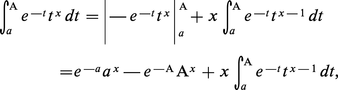
Par récurrence, on en déduit facilement :

cette relation permet de définir Γ(x) pour x réel négatif, − n < x < − n + 1. On a ainsi défini Γ(x) pour tout nombre réel x qui n'est pas un entier négatif ou nul ;

La fonction ln Γ est convexe sur ]0, +∞] ; en effet, l'inégalité de Schwarz montre que :

d'où (ln Γ)″ ≥ 0. A fortiori, la fonction Γ est convexe. Comme Γ (2) = Γ (1) = 1, la fonction Γ atteint son minimum sur R*₊ en un point compris entre 1 et 2. La figure représente le graphe de cette fonction.

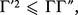
Formules d'Euler et de Weierstrass

Pour n tendant vers l'infini,

tend vers e^-t pour tout t, et cela suggère la formule (qu'il faut, bien entendu, démontrer rigoureusement) :

la seconde intégrale s'obtenant en faisant le changement de variable t = nu dans la première. Or, un calcul facile montre que :

d'où la formule d'Euler :

Pour transformer cette expression, on peut écrire :

or la quantité :

tend vers une limite γ (la célèbre constante d'Euler γ ∼ 0,577 2) lorsque n tend vers l'infini. Divisant chacun des termes du produit (x + 1)...(x + n) par l'entier correspondant pris dans n !, on a donc :

puisque le produit infini est convergent ; ce développement en produit infini a été obtenu par Weierstrass.

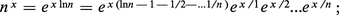
Comportement asymptotique

Le comportement de la fonction gamma lorsque la variable x tend vers l'infini est décrit par la formule de Stirling :

qui donne, en particulier, un « infiniment grand » équivalent à la factorielle :

on peut d'ailleurs préciser plus étroitement le comportement asymptotique de Γ(x) (cf. calculs asymptotiques).

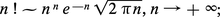
Indiquons maintenant une formule due à Legendre pour p = 2 et à Gauss dans le cas[...]