GÉOMÉTRIE ALGÉBRIQUE

Applications régulières

Soient X ⊂ k^m et Y ⊂ kⁿ des ensembles algébriques affines ; une application u de X dans Y est dite régulière si les coordonnées u₁(x), u₂(x), ..., u_n(x) de u(x) sont des fonctions polynomiales des coordonnées du point x de X. En particulier, les applications régulières de X dans k, encore appelées fonctions régulières sur X, sont les fonctions polynomiales des coordonnées d'un point de X ; elles forment un sous-anneau de l'anneau de toutes les applications de X dans k, et ce sous-anneau est visiblement isomorphe au quotient de l'anneau des polynômes k[T₁, T₂, ..., T_n]par l'idéal des polynômes qui s'annulent sur X.

Il est clair que la composée de deux applications régulières est une application régulière. En particulier, une application régulière u : X → Y définit un homomorphisme f ↦ f ∘ u, de l'anneau des fonctions régulières sur Y dans l'anneau des fonctions régulières sur X. Un isomorphisme d'un ensemble algébrique X sur un autre Y est une application bijective de X sur Y, qui est régulière ainsi que sa réciproque ; il définit un isomorphisme de l'anneau des fonctions régulières sur Y sur l'anneau des fonctions régulières sur X.

On trouvera ci-après quelques exemples d'applications régulières.

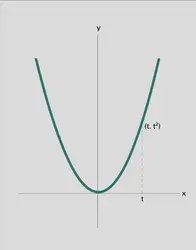
– Paramétrisation d'une parabole . Considérons l'application u de la droite k dans le plan k² définie par u(t) = (t, t²). L'image u(k) est la parabole X d'équation y = x², et u définit une bijection de k sur X, réciproque de l'application (x, y) ↦ x ; on a donc un isomorphisme de la droite k sur la parabole X.

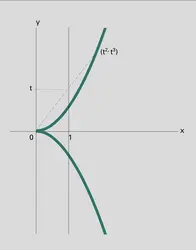
– Cissoïde. L'application v : t ↦ (t², t³) de k dans k² est aussi une application régulière. Elle applique la droite k bijectivement sur son image, qui est la « parabole semi-cubique » (ou cissoïde) Y d'équation y²= x³ ; mais ce n'est pas un isomorphisme de k sur Y, car la bijection réciproque v′, définie par v′(x, y) = y/x si x ≠ 0 et v′(0, 0) = 0 n'est pas une application régulière. En fait on peut montrer que la cissoïde Y n'est pas isomorphe à une droite en observant que son anneau de fonctions régulières n'est pas intégralement clos (la fraction z = y/x vérifie l'équation z² = x, donc est entière sur cet anneau, sans y appartenir, cf. anneaux commutatifs), et ne peut par suite être isomorphe à l'anneau k[T] des fonctions régulières sur k.

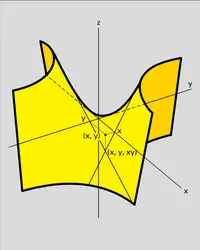
– Paraboloïde. L'application rationnelle (x, y) ↦ (x, y, xy) du plan k² dans l'espace k³ définit un isomorphisme du plan sur le paraboloïde d'équation z = xy.

Pour définir les applications régulières d'un ensemble algébrique projectif X ⊂ P_m(k) dans un autre Y ⊂ P_n(k), on procède de la même façon. Une application u de X dans Y est régulière si les coordonnées homogènes de u(x) peuvent s'exprimer par des polynômes homogènes u₀, u₁, ..., u_n, tous de même degré par rapport aux coordonnées homogènes de x ; notons que ces polynômes ne peuvent s'annuler simultanément pour x ∈ X. Si maintenant X ⊂ k^m est affine et Y ⊂ P_n(k) est projectif, les applications régulières de X dans Y sont définies en donnant les coordonnées homogènes sur Y comme fonctions polynomiales (ne s'annulant pas simultanément) des coordonnées sur X ; quant aux applications régulières de Y dans X, ce sont les applications constantes (les polynômes homogènes de degré 0 sont les seuls à être constants sur chaque droite issue de l'origine dans kⁿ⁺¹).

Par exemple, l'application α_n de kⁿ dans P_n(k) qui transforme (x₁, x₂, ..., x_n) en le point de coordonnées homogènes (1, x₁, ..., x_n) est régulière ; elle définit une bijection de kⁿ sur le complémentaire de l'hyperplan d'équation homogène x₀= 0 dans P_n(k). Tout ensemble algébrique X de kⁿ s'identifie par α_n à la partie d'un ensemble algébrique X̄ de P_n(k) où x₀≠ 0 ; si les équations de X̄ sont :

On peut généraliser l'exemple précédent et l'on peut ainsi définir pour tout couple (n, d) d'entiers naturels une application régulière de P_n(k) dans P_e(k) dans laquelle e = (n + 1)(n + 2)... (n + d)/d ! − 1, de manière à obtenir un isomorphisme de P_n(k) sur un ensemble algébrique V_n,d dans P_e(k) (la variété de Veronese) ; les coordonnées homogènes du transformé de x sont tous les monômes de degré d par rapport aux coordonnées homogènes de x.

Applications rationnelles

En remplaçant les polynômes par des fractions rationnelles dans tout ce qui précède, on obtient des « applications » non partout définies en général (car les dénominateurs peuvent s'annuler ; il y a donc un abus de langage à parler d'applications) ; ce sont les applications rationnelles. Nous ne donnons de définition précise que dans le cas des fonctions rationnelles (applications rationnelles à valeur dans k). Considérons d'abord un ensemble algébrique affine X dans kⁿ ; une fonction rationnelle f sur X est définie par une fraction P/Q ∈ k(T₁, T₂, ..., T_n), dont le dénominateur ne s'annule pas identiquement sur X ; c'est l'application x ↦ P(x)/Q(x) de l'ensemble U = {x ∈ X | Q(x) ≠ 0} dans k. De même, pour définir une fonction rationnelle sur un ensemble algébrique projectif X ⊂ P_n(k) on prend une fraction P/Q en coordonnées homogènes, avec P et Q homogènes de même degré (pour avoir une fonction constante sur les droites issues de O dans kⁿ⁺¹) et Q non identiquement nul sur X.

La composée de deux applications rationnelles f de X dans Y et g de Y dans Z peut se définir si l'ensemble des points x de X tels que f soit définie en x et g en f(x) n'est contenu dans aucun ensemble algébrique strictement plus petit que X ; c'est encore une application rationnelle. Une équivalence birationnelle entre X et Y est un couple (u, v) où u est une application rationnelle de X dans Y et v une application rationnelle de Y dans X, les composés v ∘ u et u ∘ v étant les applications identiques de X et Y respectivement.

Par exemple (x, y) ↦ y/x est une fonction rationnelle dans le plan k², définie dans le complémentaire de la droite d'équation x = 0. Sa restriction à la courbe d'équation y²= x³ est une fonction rationnelle définie en dehors de l'origine ; on voit que la cissoïde est birationnellement équivalente à la droite (sans lui être isomorphe ; cf. exemple supra et ). D'une manière générale, on dit qu'une courbe algébrique est unicursale si elle est birationnellement équivalente à la droite k (cf. courbes algébriques). Les fractions x₁/x₀, x₂/x₀, ..., x_n/x₀ définissent une application rationnelle de P_n(k) dans kⁿ ; cette application est définie dans le complémentaire de l'hyperplan d'équation homogène x₀= 0 et donne (avec α_n ; cf. supra) une équivalence birationnelle entre P_n(k) et kⁿ. De même, tout ensemble algébrique affine est birationnellement équivalent à sa complétion projective.