GÉOMÉTRIE DIFFÉRENTIELLE CLASSIQUE

Formes fondamentales sur une surface

On appelle première forme fondamentale sur une surface S la forme quadratique Φ qui, à tout vecteur V tangent à S en M, associe le carré de sa longueur, soit :

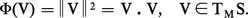
Si au voisinage de M la surface S admet pour représentation paramétrique (u, v) ↦ ϕ (u, v), on écrit :

et on a :en posant :justifions ces notations. Si γ est un arc paramétré, dont le vecteur vitesse en M est égal à V, qui se factorise sous la forme γ = ϕ ∘ f (avec les notations du chapitre précédent), alors on a :et par suite :

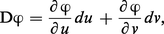
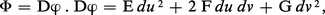
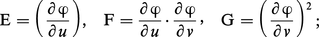
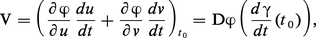
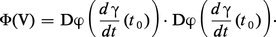
Définissons maintenant la deuxième forme fondamentale ; il sera pour cela nécessaire d'orienter la surface. Si la représentation paramétrique ϕ : U → S, U ⊂ R² est régulière en tout point M de ϕ(U), le produit vectoriel :

où m = ϕ^-1(M) ∈ U, est non nul ; on peut donc associer à chaque point M de ϕ(U) un vecteur unitaire n normal à S de même sens que le produit vectoriel précédent, c'est-à-dire on oriente la surface. Si un arc paramétré :se factorise sous la forme γ = ϕ ∘ f (cf. infra), alors le produit scalaire :où D²ϕ est la dérivée seconde de ϕ, ne dépend que du vecteur tangent :en effet, on a :d'où :en posant :

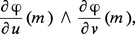
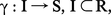
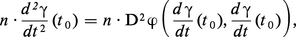
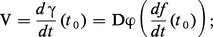
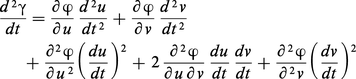
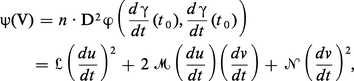
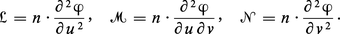
La forme quadratique ψ : V ↦ ψ(V) est appelée la deuxième forme fondamentale de la surface. On démontre que la quantité :

est indépendante de la représentation paramétrique. En particulier, pour la représentation paramétrique z = g(x, y) utilisée dans le chapitre précédent (avec p = q = 0 en M), on a :ce scalaire K s'appelle la courbure totale, ou courbure de Gauss, en M. Suivant le signe de K, le point est elliptique, hyperbolique ou parabolique (cf. chap. 5, Position par rapport au plan tangent) ; remarquons que, puisque la forme quadratique Φ est définie positive, le signe de K est celui de LN − M².

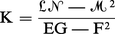
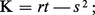
C. Gauss a démontré que la courbure totale était déterminée par E, F, G et leurs dérivées partielles premières. Étant donné deux surfaces S et S′, on appelle isométrie locale de S dans S′ un difféomorphisme d'un ouvert U de E₃ dans E₃, appliquant S ∩ U dans S′ et transformant en chaque point M de S ∩ U la première forme fondamentale de S en la première forme fondamentale de S′ ; par suite, une isométrie locale laisse invariante la courbure totale. En particulier, une surface S telle qu'il existe en chaque point M ∈ S une isométrie d'un voisinage de ce point dans S sur un ouvert plan est dite applicable sur le plan ; puisque, pour un plan, la deuxième forme fondamentale est nulle, la courbure totale d'une surface applicable sur un plan est nulle. On démontre que toute surface à courbure totale nulle est une surface développable et que toute surface développable est applicable sur le plan.

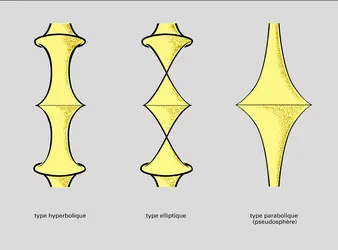
Plus généralement, on montre que si deux surfaces S et S′ ont une courbure totale constante (cette constante étant la même pour les deux surfaces), il existe des isométries locales de S sur S'. Si la courbure totale est une constante positive, on dit que la surface est une surface sphérique ; parmi ces surfaces figurent la sphère, et les surfaces sphériques de révolution du type hyperbolique et du type elliptique. Si la courbure totale est constante négative, on a les surfaces pseudosphériques ; celles qui sont de révolution se répartissent en trois types indiqués par la figure.

Enfin, signalons qu'on démontre qu'une isométrie locale qui conserve aussi la deuxième forme fondamentale est la restriction d'un déplacement euclidien ; par suite, l'ensemble des deux formes fondamentales caractérise localement une surface.