GROUPES (mathématiques) Groupes classiques et géométrie
Article modifié le
Le groupe orthogonal
On suppose donné sur E un produit scalaire : c'est une application bilinéaire :
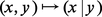
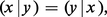

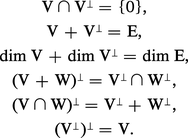
L'exemple classique de produit scalaire dans Rn est :
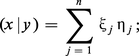
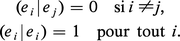
Un espace vectoriel E muni d'un produit scalaire est ce qu'on appelle un espace euclidien ; sur un même espace vectoriel E, il y a une infinité de produits scalaires non proportionnels, donnant une infinité de structures d'espace euclidien pour lesquelles les notions d'orthogonalité sont distinctes ; toutefois tous ces espaces sont isomorphes, en vertu de l'existence des bases orthonormales. On suppose dans ce qui suit que le produit scalaire est fixé, et on pose ∥x∥ =(x|x)1/2 (longueur du vecteur x).
On appelle similitude de E une transformation linéaire u ∈ GL(E) telle que :


Les similitudes forment un sous-groupe GO(E) ⊂ GL(E), et u ↦ μ(u) est un homomorphisme de ce groupe sur le groupe multiplicatif R *+ des nombres réels > 0 ; son noyau O(E) est appelé le groupe orthogonal de E (pour le produit scalaire considéré) ; c'est donc le sous-groupe de GL(E) formé des u tels que :
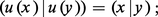
Toute homothétie hλ est une similitude de multiplicateur λ2 ; toute similitude de multiplicateur μ s'écrit d'une seule manière hλ ( v, où λ = √μ et v ∈ O(E) ; GO(E) est produit direct du groupe O(E) et du groupe multiplicatif Z+(E) des homothéties de rapport > 0, isomorphe à R *+.
Pour une transformation orthogonale de matrice U, on a, d'après la formule (1), (det U)2 = 1 ; le sous-groupe O+(E), ou SO(E), des transformations orthogonales de déterminant l (aussi appelées rotations) est d'indice 2 dans O(E). Les similitudes appartenant au sous-groupe :

Lorsque E = Rn, on suppose toujours que Rn est muni du produit scalaire classique, et on écrit O(n, R) [resp. O+(n, R) ou SO(n, R)] au lieu de O(Rn) [resp. O+(Rn)] et on l'identifie avec le groupe des matrices orthogonales (i.e. telles que tU = U-1). Si E est de dimension n, le groupe O(E) est isomorphe à O(n, R).
Générateurs du groupe orthogonal
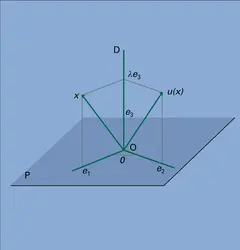
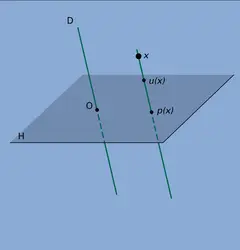
Les involutionsu de GL(E) qui appartiennent à O(E) sont celles pour lesquelles les sous-espèces propres V+ et V- (cf. Générateurs, in chap. 1) sont orthogonaux : on dit encore qu'une telle involution est une symétrie orthogonale par rapport à V+. Lorsque V+ est un hyperplan H, on dit encore réflexion orthogonale de droite V- = H⊥. Si dim E = n, toute transformation orthogonale est produit de n réflexions orthogonales au plus. Lorsque V+ est de dimension n − 2, on dit que l'involution est un renversement d'axe V- ; pour n ≥ 3, toute rotation est produit de n renversements au plus. Tout renversement est un commutateur de O+(E) si n ≥ 3 : en effet, soit (e1, e2) une base orthonormale de V-, et posons V+ = Re3 ⊕ W, où W est orthogonal à e3 ; on peut écrire u = v1v2, où v1 (resp. v2) est le renversement d'axe Re1 ⊕ Re3 (resp. Re2 ⊕ Re3) ; comme v2 est conjugué de v1 dans O+ (E) [cf. infra, Propriétés de transitivité et de conjugaison]et comme v1 = v-11, on a u = v-11sv1s-1 pour un s ∈ O+(E). On en conclut que O+(E) est son propre groupe des commutateurs et le groupe des commutateurs de O(E).
Le centre Z0 de O(E) est formé de l'identité et de la symétrie x ↦ − x. Si n est pair, Z0 est aussi le centre de O+(E) ; sinon, le centre de O+(E) est réduit à l'identité et O(E) est le produit direct Z0 × O+(E).
Propriétés de transitivité et de conjugaison
Pour que deux sous-espaces vectoriels V1, V2 de E soient transformés l'un de l'autre par une transformation orthogonale, il faut et il suffit qu'ils aient même dimension ; il existe alors une rotation u telle que V2 = u(V1). Les symétries orthogonales par rapport à V1 et V2 sont alors conjuguées.
Le groupe O(2, R) et les angles
Pour une matrice U d'ordre 2, le calcul montre que la relation (1) équivaut à dire que U peut prendre l'une des deux formes :

Les matrices U1 (resp. U2) sont celles des similitudes directes (resp. inverses). On déduit de ces formules que le groupe GO+(R2) des similitudes directes est commutatif, donc aussi le groupe O+(R2) des rotations ; GO+(R2) opère de façon simplement transitive dans R2 − {0}. On voit aussi que :


On appelle groupe des angles un groupe u isomorphe à O+(R2) (donc à U) mais noté additivement ; il n'y a, par suite, pas de distinction essentielle à faire entre les notations d'angle et les notations de rotation plane, bien qu'il soit commode de parler de la « rotation d'angle θ » et de la noter :

Puisque, par définition, r est un isomorphisme de u sur O+(2, R), on a :

Par définition, les éléments α et β dans la matrice :
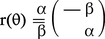
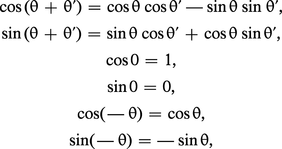
Pour deux vecteurs x et y de R2 de même longueur ∥x∥ = ∥y∥ ≠ 0, il existe une rotation u et une seule telle que u(x) = y ; l'angle θ de cette rotation est appelé l'angle de y avec x et noté (x, y). Si les deux vecteurs sont unitaires, on a cos θ = (x | y).
Si x, y, z sont trois vecteurs de même longueur dans R2, on a :

Le groupe des angles u contient des éléments d'ordre fini : par exemple, l'angle droit δ qui correspond au nombre complexe i ∈ U ou à la matrice :



Structure des transformations orthogonales
Pour toute transformation orthogonale u ∈ O(E), il y a une décomposition de E en sous-espaces deux à deux orthogonaux V, W, P1, P2..., Pr stables par u et tels que :
a) la restriction de u à V est l'identité ;
b) la restriction de u à W est la symétrie x ↦ − x ;
c) chacun des Pj est un plan (espace de dimension 2) et la restriction uj de u à Pj est une rotation distincte de l'identité et de x ↦ − x.
Si Ψj est une isométrie de P sur R2, il existe un angle θj distinct de 0 et de 2δ tel que uj = Ψj-1r(θj)Ψj, et θj est déterminé « au signe près » indépendamment du choix de Ψj ; les valeurs propres de u sont 1 (de multiplicité dim V), − 1 (de multiplicité dim W) et les e±iθj (ces dernières peuvent être multiples si θj = ± θk pour j ≠ k).
On a det (u) = (− 1)dim W ; par suite, si u ∈ O+(E) et si dim E est impair (resp. u ∉ O+(E) et dim E pair), W est nécessairement de dimension paire (resp. impaire) ; donc V ne peut être réduit à 0, en d'autres termes il existe au moins un vecteur x ≠ 0 invariant par u.
Simplicité du groupe O+(3, R)
Montrons que tout sous-groupe distingué N de O+(3, R) non réduit à l'identité est nécessairement égal à O+(3, R). Supposons donc qu'il existe u ≠ 1E dans N, de sorte que (cf. supra, Structure des transformations orthogonales) il existe une droite D dont tous les points sont invariants par u, et la restriction de u au plan P = D⊥ est une rotation d'angle θ ≠ 0 (déterminé « au signe près »). Distinguons trois cas :
a) Cos θ = − 1 ou θ = 2δ, autrement dit u est un renversement ; mais, comme N est distingué, il contient tous les renversements (cf. supra, Propriétés de transitivité et de conjugaison, in chap. 2), et donc il est égal à O+(3, R) (cf. supra, Générateurs du groupe orthogonal).
b) Cos θ < 0. Soit e3 un vecteur de longueur 1 dans D, e1 un vecteur de longueur 1 dans P et e2 = u(e1) ∈ P ; on a (e1 | e2) = Cos θ < 0. Considérons un vecteur x = λe3 + e1 ; on a u(x) = λe3 + e2, donc (x | u(x)) = λ2 + Cos θ, et, en prenant λ = (− Cos θ)1/2, on obtient un vecteur tel que (x | u(x)) = 0. Soit alors v le renversement d'axe Rx ; uvu-1 est le renversement d'axe Ru(x). Comme N est distingué,

c) 0 < Cos θ < 1. On voit aisément qu'il existe un entier n > 0 tel que Cos nθ < 0 ; comme un ∈ N, il suffit d'appliquer le cas b à un et la démonstration est achevée.
Les groupes O+(n, R) pour n ≥ 4
En utilisant la simplicité du groupe O+(3, R), on peut, par un raisonnement tout aussi élémentaire mais assez long, prouver que :

Spineurs
L'algèbre des quaternions sur R se généralise de la façon suivante. Pour tout entier n ≥ 2, il existe une algèbre Cn sur R, de dimension 2n, dite algèbre de Clifford d'indice n, qui est engendrée, en tant qu'algèbre, par l'élément unité 1 et n éléments ej (1 ≤ j ≤ n) identifiés à la base canonique de Rn, et qui sont assujettis à vérifier les conditions suivantes :

On montre que les 2n produits :


Le groupe multiplicatif engendré dans C+n par les produits ab, où a et b varient dans Rn − {0} et sont de longueur 1, est noté Spin(n) ; on montre qu'il existe un homomorphisme surjectif et un seul σ : Spin(n) → O+(n, R) tel que σab = sasb ; le noyau de cet homomorphisme est formé de l'identité et de − 1, mais Spin(n) n'est pas produit semi-direct de ce sous-groupe et d'un groupe isomorphe à O+(n, R). Lorsque l'on considère C+n comme un espace vectoriel sur lequel Spin(n) opère par multiplication à gauche, les éléments de C+n sont appelés spineurs (cf. groupes [mathématiques] – Groupes de Lie).
Accédez à l'intégralité de nos articles
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
Écrit par
- Jean DIEUDONNÉ : membre de l'Académie des sciences
Classification
Médias
Autres références
-
ALGÈBRE
- Écrit par Jean-Luc VERLEY
- 7 145 mots
La structure de groupe est une des structures algébriques les plus simples et, sans conteste, la plus importante des mathématiques modernes. Son universalité ne s'arrête pas là : le psychologue Piaget a mis en évidence le rôle essentiel joué par cette notion dans les mécanismes mêmes de la pensée, et... -
BOREL ARMAND (1923-2003)
- Écrit par Pierre CARTIER
- 795 mots
En 1992, le mathématicien Armand Borel a reçu le prix international Balzan « pour ses contributions fondamentales à la théorie des groupes de Lie, des groupes algébriques et des groupes arithmétiques, et pour son action inlassable en faveur de la recherche mathématique et de la propagation...
-
BURNSIDE WILLIAM SNOW (1852-1927)
- Écrit par Bernard PIRE
- 394 mots
Mathématicien britannique, spécialiste de la théorie des groupes. Né le 2 juillet 1852 à Londres (Grande-Bretagne) d'un père écossais, William Snow Burnside fait ses études supérieures au Pembroke College de l'université de Cambridge, dont il est diplômé en 1875 et où il effectue ses recherches...
-
CAUCHY AUGUSTIN-LOUIS (1789-1857)
- Écrit par Jean DIEUDONNÉ
- 1 402 mots
- 1 média
...valeurs propres d'une matrice symétrique d'ordre supérieur à 3, et il partage avec Binet la découverte de la formule donnant le produit de deux déterminants. Il a été aussi le premier à dégager clairement la notion de groupe de permutations et on lui doit les premiers résultats non triviaux de la théorie des... - Afficher les 34 références
Voir aussi
- GROUPE SIMPLE
- COSINUS
- TRIGONOMÉTRIE
- SINUS, mathématiques
- CENTRALISATEUR, mathématiques
- COMMUTATEUR, mathématiques
- GROUPE LINÉAIRE GÉNÉRAL
- HYPERPLAN
- NOMBRES RATIONNELS
- ERLANGEN PROGRAMME D'
- INVOLUTION, mathématiques
- GÉOMÉTRIES NON EUCLIDIENNES
- TRANSFORMATIONS GÉOMÉTRIQUES
- PRODUIT SCALAIRE
- HOMOTHÉTIE
- TRIGONOMÉTRIE HYPERBOLIQUE
- ESPACE EUCLIDIEN
- SPINEUR
- GROUPE SYMPLECTIQUE
- GROUPE UNITAIRE
- TRANSITIVITÉ
- ISOTROPE, mathématiques
- WITT INDICE DE
- GROUPE ORTHOGONAL
- ORTHOGONALITÉ
- BASE ORTHONORMALE
- ISOMÉTRIE, mathématiques
- GROUPE UNIMODULAIRE ou GROUPE LINÉAIRE SPÉCIAL
- TRANSVECTION
- ANGLE
- GÉOMÉTRIE ELLIPTIQUE
- RÉFLEXION, mathématiques
- SIMILITUDE, mathématiques
- GROUPE DE TRANSFORMATIONS
- GROUPE SPÉCIAL UNITAIRE
- ROTATION, mathématiques