GROUPES (mathématiques) Groupes de Lie
- 1. La structure des groupes de Lie généraux
- 2. Groupes de Lie compacts et groupes semi-simples
- 3. Actions des groupes de Lie
- 4. Représentations linéaires de dimension finie des groupes de Lie
- 5. Algèbres de Lie
- 6. Algèbres de Lie semi-simples
- 7. Algèbres semi-simples complexes et leurs formes réelles
- 8. Représentations linéaires de dimension infinie
- 9. Généralisations
- 10. Bibliographie
Groupes de Lie compacts et groupes semi-simples
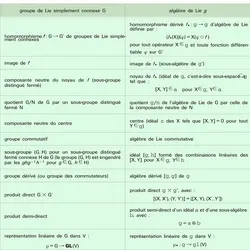
Soit G un groupe de Lie connexe ; il existe alors dans G un sous- groupe compact maximal K et un nombre fini de sous-groupes fermés H1, ..., Hp isomorphes à R, tels que l'application :
On peut citer deux exemples : dans SL(n, R), le groupe SO(n, R) est un sous-groupe compact maximal ; dans GL(n, C), le groupe U(n, C), aussi noté U(n), est un sous-groupe compact maximal.
Le revêtement universel d'un groupe de Lie compact K est de la forme K′ × Rn, où K′ est compact, semi-simple et simplement connexe. Tout groupe compact semi-simple et simplement connexe est produit direct de sous-groupes compacts simplement connexes et simples (c'est-à-dire n'ayant pas de sous-groupe fermé distingué distinct d'eux-mêmes et de dimension strictement positive) ; leurs centres sont finis, et les sous-groupes distingués fermés d'un groupe simple sont contenus dans le centre.
Groupes classiques simples
Encyclopædia Universalis France
Les groupes simples compacts simplement connexes sont explicitement connus (classification de Killing- É. Cartan) : il y a d'abord quatre séries infinies de groupes classiques .
Les groupes de types B, C peuvent être définis pour m ≥ 1 et ceux du type D pour m ≥ 2, mais on n'obtient pas de groupes essentiellement nouveaux, car on a les isomorphismes A1 ≃ B1 ≃ C1, B2 ≃ C2 et A3 ≃ D3, et le groupe de type D2 est isomorphe au produit de deux groupes de type A1. Il faut enfin préciser que le groupe unitaire U(m, H) sur le corps des quaternions H se rapporte à une forme unitaire positive non dégénérée.
Il existe en outre cinq groupes exceptionnels, notés :
On verra plus loin (chap. 2, 3 et 4) d'autres précisions sur ces groupes. Mentionnons ici que l'algèbre de cohomologie des groupes classiques est entièrement déterminée sur l'anneau des entiers ou sur un corps premier ; on connaît aussi les groupes d'homotopie :
Les groupes semi-simples complexes correspondent biunivoquement aux groupes semi-simples compacts, tout groupe semi-simple compact K étant sous-groupe compact maximal d'un groupe semi-simple complexe G, déterminé à isomorphie près, de dimension complexe égale à la dimension de K et dont le centre est celui de K (cf. chap. 6 et 7). Pour les groupes compacts classiques, les groupes simples complexes simplement connexes correspondants sont les suivants :
La situation est plus compliquée pour les groupes semi-simples réels non compacts (et non sous-jacents à un groupe semi-simple complexe) ; ils peuvent avoir un centre infini (discret) et ne contenir aucun sous-groupe compact distinct de {e} (par exemple le revêtement universel de SL(2, R)). On se limitera ici aux groupes semi-simples réels dont le centre est fini (le quotient d'un groupe semi-simple par son centre, cf. chap. 5, a toujours un centre réduit à e). Un tel groupe Gc de dimension n est sous-groupe fermé d'un groupe semi-simple complexe Gc, bien déterminé à isomorphie près (le « complexifié » de G, cf. chap.[...]
- 1. La structure des groupes de Lie généraux
- 2. Groupes de Lie compacts et groupes semi-simples
- 3. Actions des groupes de Lie
- 4. Représentations linéaires de dimension finie des groupes de Lie
- 5. Algèbres de Lie
- 6. Algèbres de Lie semi-simples
- 7. Algèbres semi-simples complexes et leurs formes réelles
- 8. Représentations linéaires de dimension infinie
- 9. Généralisations
- 10. Bibliographie
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
Écrit par
- Jean DIEUDONNÉ : membre de l'Académie des sciences
Classification
Pour citer cet article
Jean DIEUDONNÉ. GROUPES (mathématiques) - Groupes de Lie [en ligne]. In Encyclopædia Universalis. Disponible sur : (consulté le )
Médias
Groupes classiques simples
Encyclopædia Universalis France
Théorie des groupes et des algèbres de Lie
Encyclopædia Universalis France
Autres références
-
ALGÈBRE
- Écrit par Jean-Luc VERLEY
- 7 143 mots
La structure de groupe est une des structures algébriques les plus simples et, sans conteste, la plus importante des mathématiques modernes. Son universalité ne s'arrête pas là : le psychologue Piaget a mis en évidence le rôle essentiel joué par cette notion dans les mécanismes mêmes de la pensée, et... -
ALGÉBRIQUES STRUCTURES
- Écrit par Jean-Marie PRUVOST-BEAURAIN
- 29 463 mots
Un groupe peut être défini indifféremment comme un monoïde (E, l) tel que tout élément de E soit symétrisable, ou comme un magma associatif unifère (E, l) tel que tout élément de E soit symétrisable, ou comme un groupoïde ayant un et un seul élément neutre. Tout semi-groupe fini est un groupe.... -
BOREL ARMAND (1923-2003)
- Écrit par Pierre CARTIER
- 795 mots
En 1992, le mathématicien Armand Borel a reçu le prix international Balzan « pour ses contributions fondamentales à la théorie des groupes de Lie, des groupes algébriques et des groupes arithmétiques, et pour son action inlassable en faveur de la recherche mathématique et de la propagation...
-
BURNSIDE WILLIAM SNOW (1852-1927)
- Écrit par Bernard PIRE
- 394 mots
Mathématicien britannique, spécialiste de la théorie des groupes. Né le 2 juillet 1852 à Londres (Grande-Bretagne) d'un père écossais, William Snow Burnside fait ses études supérieures au Pembroke College de l'université de Cambridge, dont il est diplômé en 1875 et où il effectue ses recherches...
- Afficher les 35 références
Voir aussi
- ORBITE, mathématiques
- GROUPE SIMPLE
- GROUPE SEMI-SIMPLE
- OPÉRATION D'UN GROUPE
- ALGÈBRES
- GROUPE RÉSOLUBLE
- CARACTÈRE, mathématiques
- REPRÉSENTATION LINÉAIRE DES GROUPES
- GROUPE ALGÉBRIQUE
- P-ADIQUES NOMBRES
- LIE ALGÈBRES DE
- BESSEL FONCTIONS DE
- AUTOMORPHE FONCTION
- GROUPE COMMUTATIF ou GROUPE ABÉLIEN
- TAYLOR FORMULE DE
- LAPLACIEN
- GROUPE ORTHOGONAL
- GROUPE UNIMODULAIRE ou GROUPE LINÉAIRE SPÉCIAL
- JACOBI IDENTITÉ DE
- ESPACE SYMÉTRIQUE
- GROUPE COMPACT
