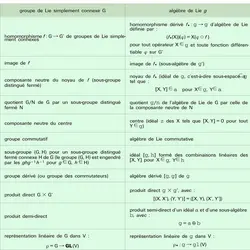
- 1. La structure des groupes de Lie généraux
- 2. Groupes de Lie compacts et groupes semi-simples
- 3. Actions des groupes de Lie
- 4. Représentations linéaires de dimension finie des groupes de Lie
- 5. Algèbres de Lie
- 6. Algèbres de Lie semi-simples
- 7. Algèbres semi-simples complexes et leurs formes réelles
- 8. Représentations linéaires de dimension infinie
- 9. Généralisations
- 10. Bibliographie
GROUPES (mathématiques) Groupes de Lie
Article modifié le
Algèbres semi-simples complexes et leurs formes réelles
Dans le chapitre 6, en partant de l' algèbre de Lie d'un groupe semi-simple compact, on a obtenu, en la complexifiant, une algèbre de Lie semi-simple complexe. Ce processus admet une réciproque, qui établit une correspondance biunivoque entre groupes connexes semi-simples complexes et groupes connexes semi-simples compacts.
L'unique méthode connue pour établir ce fait est due à Killing et É. Cartan, et est fort longue : on commence par démontrer, dans une algèbre semi-simple complexeg de dimension n sur C, l'existence d'une sous-algèbre commutative maximale h (sous-algèbre de Cartan) telle que la relation ad(X)(h) ⊂ h entraîne X ∈ h. En étudiant la représentation adjointe H ↦ ad(H) de h dans l'espace vectoriel g, on arrive alors à décomposer g en somme directe de h et de sous-espaces CXα de dimension 1, où les Xα vérifient les relations (13) à (16). On voit aisément que l'espace vectoriel réel u engendré par les iHα, les Xα − X−α et les i(Xα + X−α) est une algèbre de Lie réelle dans laquelle la forme de Killing est négative non dégénérée ; donc u est l'algèbre de Lie d'un groupe compact semi-simple U, et g = u ⊕ iu. Les iHα engendrent une sous-algèbre (réelle) commutative maximale t de u (correspondant à un tore maximal T de U), et on a h = t ⊕ it.
Si l'on choisit une base (αj), avec 1 ≤ j ≤ m, du système des racines de g, la sous-algèbre (complexe) n+ (resp. n-) de g ayant pour base les Xα pour α > 0 (resp. α < 0) est une sous-algèbre nilpotente ; on a :
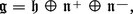
Dans SL(n, C), par exemple, un groupe de Borel est le groupe trigonal large supérieur T(n, C) (cf. chap. 1).
Le groupe de Borel permet de donner une expression explicite de la représentation linéaire de G correspondant à une représentation linéaire de g de poids dominant ω. Supposons, pour simplifier, G simplement connexe, et soit M le sous-groupe connexe de G correspondant à h, qui est isomorphe à (C*)m (« groupe de type multiplicatif ») ; on déduit de ω un homomorphisme ψω : M → C* défini par :
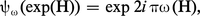
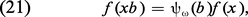
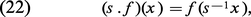
On dit qu'une algèbre semi-simple g0 sur R est une forme réelle de g si g est isomorphe à la complexifiée :
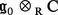
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
Écrit par
- Jean DIEUDONNÉ : membre de l'Académie des sciences
Classification
Médias
Autres références
-
ALGÈBRE
- Écrit par Jean-Luc VERLEY
- 7 145 mots
La structure de groupe est une des structures algébriques les plus simples et, sans conteste, la plus importante des mathématiques modernes. Son universalité ne s'arrête pas là : le psychologue Piaget a mis en évidence le rôle essentiel joué par cette notion dans les mécanismes mêmes de la pensée, et... -
BOREL ARMAND (1923-2003)
- Écrit par Pierre CARTIER
- 795 mots
En 1992, le mathématicien Armand Borel a reçu le prix international Balzan « pour ses contributions fondamentales à la théorie des groupes de Lie, des groupes algébriques et des groupes arithmétiques, et pour son action inlassable en faveur de la recherche mathématique et de la propagation...
-
BURNSIDE WILLIAM SNOW (1852-1927)
- Écrit par Bernard PIRE
- 394 mots
Mathématicien britannique, spécialiste de la théorie des groupes. Né le 2 juillet 1852 à Londres (Grande-Bretagne) d'un père écossais, William Snow Burnside fait ses études supérieures au Pembroke College de l'université de Cambridge, dont il est diplômé en 1875 et où il effectue ses recherches...
-
CAUCHY AUGUSTIN-LOUIS (1789-1857)
- Écrit par Jean DIEUDONNÉ
- 1 402 mots
- 1 média
...valeurs propres d'une matrice symétrique d'ordre supérieur à 3, et il partage avec Binet la découverte de la formule donnant le produit de deux déterminants. Il a été aussi le premier à dégager clairement la notion de groupe de permutations et on lui doit les premiers résultats non triviaux de la théorie des... - Afficher les 34 références
Voir aussi
- ORBITE, mathématiques
- GROUPE SIMPLE
- GROUPE SEMI-SIMPLE
- OPÉRATION D'UN GROUPE
- ALGÈBRES
- GROUPE RÉSOLUBLE
- CARACTÈRE, mathématiques
- REPRÉSENTATION LINÉAIRE DES GROUPES
- GROUPE ALGÉBRIQUE
- P-ADIQUES NOMBRES
- LIE ALGÈBRES DE
- BESSEL FONCTIONS DE
- AUTOMORPHE FONCTION
- GROUPE COMMUTATIF ou GROUPE ABÉLIEN
- TAYLOR FORMULE DE
- LAPLACIEN
- GROUPE ORTHOGONAL
- GROUPE UNIMODULAIRE ou GROUPE LINÉAIRE SPÉCIAL
- JACOBI IDENTITÉ DE
- ESPACE SYMÉTRIQUE
- GROUPE COMPACT