INFINI, mathématiques

Les infinitésimaux

Aux yeux de Leibniz, un calcul est défini par la donnée de ses éléments (les termes du calcul, par exemple les entiers dans l'arithmétique élémentaire) et par celle des lois de composition définies sur l'ensemble de ses éléments : nous dirions aujourd'hui qu'il est défini par le couple (E, {Ω}) dans lequel E désigne un ensemble non vide et {Ω} une classe d'opérations. Dans le cas du calcul infinitésimal, de quoi se compose E ? Écrivons, dans la notation usuelle, l'expression :

Elle comporte une quantité finie f (x) et une quantité « dx » dont le statut demande à être examiné. Les lois formelles de l'opération notée ∫ exigent que la différence |x − dx| diffère de x « d'aussi peu que l'on voudra ». Or, dans le champ des grandeurs usuelles, un calcul n'est effectuable que si les grandeurs considérées sont homogènes. Soit par exemple le matériau mis en œuvre dans la géométrie d'Euclide : points, lignes, surfaces, volumes. Nous disposons ici de quatre ensembles distincts. Si à un ensemble de points distingué sur une droite nous ajoutons des points, nous obtiendrons un nouvel ensemble de points. Pour parler le langage de Leibniz (Die mathematische Schriften, t. V, p. 322), nous augmenterons la « quantité » de l'ensemble initial. Il en ira de même si à un segment de droite nous ajoutons un élément de droite, à une surface un élément de surface, etc. En revanche, nous n'augmenterons pas la quantité initialement donnée si à une ligne nous ajoutons un point, à une surface une ligne, etc. Dans le langage leibnizien, points, lignes, surfaces, volumes sont « incomparables ». Selon l'opération nommée « adjonction d'éléments », nous pourrons dire qu'un point est « négligeable » par rapport à une ligne, une ligne « négligeable » par rapport à une surface, etc. Ici se trouve marquée l'entrée du chemin qui, pour un temps au moins, devait, tant bien que mal, donner droit de cité aux « éléments infinitésimaux ». Le concept d'« incomparabilité » est sur ce point décisif. Il ouvrait, dès l'origine, la possibilité d'une extension (que Leibniz n'a pas réalisée, et c'est pourquoi la notion d'« élément infinitésimal » reste tellement ambiguë aux commencements du « calcul ») qui eût conduit, si elle avait été poursuivie, à construire, comme champ de l'analyse, une extension non archimédienne du système des nombres réels. Ce programme a été réalisé par A. Robinson (Non-Standard Analysis). Leibniz énonce (op. cit., t. V, p. 322) qu'on « n'augmente pas la quantité d'une ligne en lui ajoutant une ligne incomparablement plus petite ». Par rapport à x, dx « se conduit » comme un point : cela veut dire que dx n'est pas « homogène à x ». C'est-à-dire qu'il n'existe pas d'entier fini n, si grand qu'on le choisisse, tel que ndx > x. D'où la conséquence, extrêmement fâcheuse : ou bien admettre, par coup de force, un nombre infini donné (ce que Leibniz refuse), ou bien construire l'extension non archimédienne permettant de composer, dans le même calcul, les grandeurs finies et leurs éléments infinitésimaux (ce que Leibniz ne pouvait faire). Cependant, comme autrefois, dans l'Antiquité grecque, lors de la « crise » des irrationnelles, l'exigence opératoire a triomphé des réticences liées aux modes usuels de représentation. Leibniz et, à sa suite, G. de L'Hospital ont adjoint au système des grandeurs usuelles (aussi petites ou aussi grandes que l'on veut, certes, mais finies) ces « objets idéaux » que sont les « infiniment petits ». Ceux-ci, ainsi que le précise Leibniz, peuvent être pris comme « des notions idéales qui abrègent le raisonnement, semblables à ce qu'on appelle racines imaginaires dans l'analyse commune ». Leibniz suggère aussi aux esprits inquiets de ne pas prendre les « infiniment petits » (ou les « infiniment grands ») dans « toute la rigueur métaphysique ». Cette réticence est instructive : elle indique que Leibniz a bien vu la difficulté, dont la solution eût été d'admettre en mathématiques un infini actuel au sein duquel les éléments « incomparables » eussent trouvé une place canonique. Mais il eût fallu alors construire rigoureusement le concept de ce champ infini. Nous savons aujourd'hui qu'une telle construction exige la mise en œuvre de moyens métamathématiques dont Leibniz ne disposait pas. Il a donc fallu se contenter ici d'un détour rusé : admettre l'« infinitésimale » comme une fiction rationnelle, indispensable à l'art d'inventer, quitte à chercher sa justification dans la métaphysique, dans la monadologie, théorie générale de l'être. La conséquence positive d'une telle admission est la distinction des « ordres de petitesse » : dx « incomparablement petit » par rapport à x, d²x « incomparablement petit » par rapport à dx, etc.

Le passage à la limite

Conséquence lourde de difficultés : l'exigence de donner un statut au concept de « passage à la limite » et au concept, solidaire, de « quantité évanouissante ». Lorsque Leibniz réfléchit au sens de l'écriture :

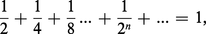
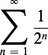
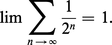
Nous pouvons l'écrire en raison de la loi de constitution de la suite (1/2ⁿ), et parce que nous disposons, sur l'ensemble des nombres réels, d'une définition purement analytique de la convergence. Il n'en allait pas de même aux origines du « calcul » où le concept de série infinie restait encore, à la fois, très opératoire et très intuitif. Aussi Leibniz interprète-t-il le signe de l'égalité en déclarant (op. cit., t. V, p. 121) qu'aussi loin que l'on poursuive la dichotomie du segment AB de longueur 1 jamais on ne dépassera la borne B (nunquam egredieris terminum B). Ce qui laisse supposer deux choses : il est toujours possible d'insérer après un terme de la suite un nouveau terme selon la même loi ; les différences entre deux termes consécutifs vont décroissant et, au voisinage de la borne B, ces différences se rapprochent de plus en plus de zéro, sans qu'il soit jamais possible de désigner la dernière d'entre elles. L'« égalité » est alors le substitut d'une inégalité, mais d'une inégalité inassignable. L'ambiguïté tient ici à ce que Leibniz manie du même mouvement deux conceptions distinctes : une conception purement ordinale (l'ordre dense de la suite 1/2ⁿ) et une conception liée à l'intuition du « quantum » (la valeur de la différence entre deux termes consécutifs). Si la première conception pouvait orienter vers la notion de limite, la seconde le conduisit, au voisinage de la borne, à proposer l'idée, à vrai dire métaphysique, de « quantité évanouissante ». Seul le principe de continuité (c'est-à-dire ici le principe de l'invariance de la loi de la série en chacun de ses termes) assure l'unité de l'« envisagement » ordinal et de l'intuition « quantitative ». Mais alors on accomplit un saut dans le domaine du « comme si ». C'est là la vertu du principe leibnizien de continuité (datis ordinatis etiam quaesita sunt ordinata : l'ordre posé dans les données doit s'observer dans leurs conséquences). Ce principe permet de rationaliser l'intuition vague de cette espèce de processus naturel que l'on nomme « passage d'un état à un autre », ou « changement d'état », et dont le mouvement local est la forme la plus simple. Dans l'analyse de ces formes de passage, Leibniz a privilégié les fonctions les mieux connues (celles qui se présentent en cinématique par exemple) : les fonctions continues. Il était alors conduit à concevoir le domaine dans lequel ces fonctions sont définies comme un « continu », bien que, sur ce point, il semble n'avoir pas distingué le concept de « continu » du concept de « partout dense ». Que l'on considère l'espace (ordre idéal des coexistences possibles), que l'on considère le temps (ordre idéal des successions possibles), que l'on considère l'ensemble organique des êtres réels (la hiérarchie des monades), dans chaque cas le lieu où se repèrent les mouvements, où se définissent les transformations, où agissent les êtres est pensé comme un « continu », une plénitude sans lacunes. Dès lors, pour le concept d'élément infinitésimal, s'opère un glissement du champ de l'arithmétique (ou mieux de l'algèbre), au champ d'une sorte de géométrie abstraite, dont les éléments seraient animés par le dynamisme propre de l'intellect. Pensée comme « incomparable » dans le premier champ, l'infinitésimale est pensée dans le second, c'est-à-dire dans ce domaine de rationalité partout dense (nommé improprement « continu »), comme moment inassignable du passage. L'état de repos sera pris comme état inassignable de mouvement ; l'arrêt d'un mouvement à sa borne (par exemple dans l'indéfinie dichotomie du segment AB) comme moment de passage inassignable à la borne, dont on dira qu'elle ne peut être atteinte qu'à la limite. Au cours de ce glissement, qu'autorise la simplification rationnelle constituée par le principe de continuité, tout se passe comme si on avait construit le domaine dans lequel il est permis de composer « grandeurs incomparables » et grandeurs ordinaires. Faute de pouvoir édifier la théorie formelle du système élargi englobant dans le même calcul grandeurs finies et éléments infinitésimaux, on a construit une représentation abstraite, un modèle consistant du domaine dans lequel s'opèrent les passages, se combinent les états, s'édifient les êtres. Dans ce mouvement, le concept de « l'incomparable » est réinvesti, mais dénaturé. Dans le modèle ainsi forgé, les êtres non homogènes sont reliés les uns aux autres par la loi de continuité. Comme le dit Leibniz, ils seront, dans ce domaine, homogônes : la ligne par rapport au point, la surface par rapport à la ligne et, généralement, « l'interminé par rapport au terminé ».

Ainsi apparaissent les contraintes inédites que l'essor du « calcul » fait peser sur le concept d'infini mathématique (et, plus généralement, sur le concept d'objet mathématique). D'abord, ainsi que l'a admirablement montré Yvon Belaval (Leibniz critique de Descartes), c'en est fait, sur ce point, de l'épistémologie cartésienne. On ne peut plus considérer un être mathématique comme formé de la composition de « natures simples » données en une intuition indivisible. En ce « continu » qui constitue le domaine fondamental de rationalité, il n'y a pas de natures simples : tout état distingué en lui y est encore composé à l'infini. Seule la loi (à la rigueur formalisable) de la composition constitue le chemin vers la connaissance. De plus, l'infini mathématique (celui de la série de terme général 1/2ⁿ par exemple) n'est plus un « mauvais infini » : il ne témoigne pas pour la limitation de l'entendement humain qui, incapable d'embrasser l'infini véritable, ne pourrait s'élever au-dessus de la considération de l'indéfini. Cet infini est inscrit dans la nature de l'opération elle-même et en celle du domaine où elle s'effectue. Dieu lui-même ne peut achever la sommation : pour lui comme pour nous l'égalité est ici une « inégalité évanouissante ». De là l'exigence d'une remise en chantier des principes de la logique : en particulier, il importe de définir le champ de validité du principe du tiers exclu si l'on veut donner au concept de quantité « évanouissante » le statut de la rationalité. Mais il y a plus. À travers les difficultés que propose un tel concept apparaissent, dans le chantier de l'analyse en voie de constitution, quelques contraintes spécifiques du champ d'objets ici envisagé. La plus fondamentale est celle-ci : comment penser en sa pureté logique la contexture des domaines où sont définies les opérations, construites les fonctions, et pour lesquels sont posés pensables et effectuables les enchaînements propres au calcul infinitésimal ? En particulier qu'en est-il du statut de concept de limite ? Quelles conditions restrictives concevoir, capables de le fonder rigoureusement ? Ces questions, bien qu'elles aient été recouvertes et masquées, jusqu'à l'époque d'A. Cauchy, par l'essor opératoire du calcul lui-même, étaient ouvertes, dès l'origine, dans cette admission, étrange mais nécessaire en son lieu, des éléments « infinitésimaux ». Dans la mise en œuvre d'une telle interrogation, le concept d'infini mathématique devait gagner son autonomie et se constituer dans le seul champ de la mathématique. La création cantorienne consacre cette autonomie.