NOMBRES (THÉORIE DES) Nombres algébriques
Article modifié le
Unités
Dans une série de courtes notes, Dirichlet (1841-1846) a étudié les unités dans des anneaux de nombres algébriques de la forme Z[θ], où θ vérifie une équation irréductible xn + a1xn-1 + ... + an = 0 à coefficients ai entiers rationnels ; si les racines de cette équation sont θ, θ1, ..., θn-1, les conjugués d'un élément f (θ) de Z[θ] sont f (θ1), ..., f (θn-1), et sa norme est le produit Nf (θ) = f (θ)f (θ1) ... f (θn-1). Les unités de Z[θ] sont les éléments f (θ) de norme ± 1 (la norme est toujours un entier rationnel, mais elle peut être négative dans ce cas général) ; parmi les unités, les racines de 1 qui appartiennent à Z[θ] sont caractérisées par |f (θ)| = |f (θ1)| = ... = |f (θn-1)| = 1. En effet, si f (θ) vérifie ces conditions, il en est de même de ses puissances f (θ)k, k ∈ N, dont tous les conjugués restent donc bornés. Or l'ensemble des éléments de Z[θ] dont les conjugués sont tous majorés par une constante M est fini, car ces éléments sont les racines d'un nombre fini d'équations de degré n (leurs coefficients sont les fonctions symétriques élémentaires des conjugués, donc ce sont des entiers rationnels majorés en fonction de M et de n) ; il n'y a donc qu'un nombre fini de puissances f (θ)k distinctes, et f (θ)l = 1 pour l convenable. Les racines de l appartenant à Z[θ] forment un groupe fini cyclique pour la multiplication ; la finitude provient du résultat précédent, et le caractère cyclique du fait que, pour tout l, il y a au plus l solutions de l'équation xl = l dans C, donc dans Z[θ] (cf. groupes (mathématiques) - Généralités). L'énoncé fondamental de Dirichlet est le suivant :
Théorème. Soit r1 le nombre de racines réelles de l'équation en θ, et 2 r2 le nombre de ses racines imaginaires (de sorte que r1 + 2 r2 = n). Il existe r = r1 + r2 − 1 unités fondamentales e1(θ), e2(θ), ..., er(θ) telles que toute unité s'écrive, d'une manière unique, sous la forme ωe1(θ)n1e2(θ)n2 ... er(θ)nr, où ω est une racine de 1 et où les exposants ni appartiennent à Z.
Autrement dit, le groupe multiplicatif des unités est le produit du groupe des racines de 1 par un groupe isomorphe à Zr.
On démontre le théorème en utilisant le plongement logarithmique ainsi défini : on indexe les racines de l'équation en θ de manière que θ1, θ2, ..., θr1 soient réelles et que θj+r2 soit complexe conjugué de θj pour r1 + 1 ≤ j ≤ r1 + r2 ; on note alors Le(θ) le vecteur (ln|e(θi)|) de Rr1+r2 (1 ≤ i ≤ r1 + r2). Ainsi e(θ) ↦ Le(θ) est un homomorphisme du groupe des unités dans Rr1+r2, et son noyau est le sous-groupe formé des racines de 1 ; l'image est un sous-groupe de Rr1+r2, et on aura démontré le théorème en prouvant que cette image est un groupe libre de rang r. Or l'image de L est discrète, car si Le(θ) reste borné, tous les conjugués de e(θ) sont majorés en valeur absolue par une constante et e(θ) ne peut prendre qu'un nombre fini de valeurs ; on sait qu'un sous-groupe discret de Rs est libre de rang ≤ s (cf. atopologie-Topologie algébrique). En écrivant que la norme de e(θ) est ± 1, on voit de plus que l'image de L est contenue dans l'hyperplan d'équation :

Le groupe des unités n'est donc fini (et réduit aux racines de 1) que si r1 = 1 et r2 = 0, ce qui donne n = 1 et θ ∈ Z, ou bien si r1 = 0 et r2 = 1, ce qui donne n = 2 ; dans ce cas, on peut se ramener à θ =√− D, avec D entier rationnel positif non divisible par 4, ou bien à θ = (1 +√− D)/2, avec D ≡ 3 (mod 4). On a vu, par exemple, que le groupe des unités de Z[i]est d'ordre 4, tandis que celui de Z[j], j racine cubique de 1, est d'ordre 6 (théorie de Kummer pour λ = 3). Lorsque θ = √D, avec D entier rationnel positif sans facteur carré, on a r1 = 2, r2 = 0 et le groupe des unités est de rang r = 1 ; toute unité s'écrit ± (T + U√D)n, où n ∈ Z et où T + U√D est une unité fondamentale. Cela revient à dire que l' équation de Pell x2 − Dy2 = N(x + y
√D) = ± 1 est résolue en posant x + y
√D = ± (T + U√D)n, et on a donc démontré l'existence de solutions pour cette équation. Pour les entiers cyclotomiques, on a, avec les notations antérieures, r1 = 0 et r2 = (λ − 1)/2 = μ, donc le groupe des unités est de rang r = μ − 1, qui est ≥ 1 à partir de λ = 5 ; la difficulté de trouver des lois de réciprocité supérieures sur le modèle des lois pour les degrés 2, 3 et 4 est liée au caractère infini de ces groupes d'unités. Pour λ = 5, r = 1 et on peut prendre le nombre réel α + α4 comme unité fondamentale ; pour λ = 7, r = 2 et un système d'unités fondamentales (réelles) est donné par (α + α-1, α3 + α-3). Pour λ = 11, r = 4, et on a le système fondamental (α + α-1, α2 + α-2, α4 + α-4, α3 + α-3). Dans le cas cyclotomique général, Kummer considère le sous-groupe du groupe des unités engendré par ± 1, α et les unités (1 − αj)/(1 − α), en prenant j = γi, γ racine primitive modulo λ et 1 ≤ i ≤ μ = (λ − 1)/2 ; ce sous-groupe a le même rang r = μ − 1 que le groupe des unités, et le quotient est donc d'ordre fini h2. En s'inspirant du travail de Dirichlet sur le nombre de classes de formes quadratiques (cf. théorie des nombres -Théorie analytique des nombres), Kummer a donné une formule pour l'ordre h du groupe des classes de diviseurs des entiers cyclotomiques ; il se sert d'une fonction analogue à la fonction zêta (cf. fonction zêta) :
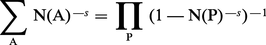

Accédez à l'intégralité de nos articles
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
Écrit par
- Christian HOUZEL : directeur de recherche au C.N.R.S., professeur à l'université de Paris-VIII-Denis-Diderot
Classification
Autres références
-
PRIX ABEL 2016
- Écrit par Yves GAUTIER
- 1 168 mots
- 2 médias
Le 15 mars 2016, l’Académie norvégienne des sciences et des lettres a décerné le prix Abel 2016 au mathématicien anglais Andrew John Wiles « pour avoir démontré de manière éclatante le dernier théorème de Fermat par le biais de la conjecture de modularité pour les courbes elliptiques semi-stables,...
-
ARITHMÉTIQUES (Diophante)
- Écrit par Bernard PIRE
- 189 mots
Diophante d'Alexandrie, parfois appelé le « père de l'algèbre », est connu par son ouvrage les Arithmétiques, qui traite des solutions des équations algébriques. On ne sait pratiquement rien de sa vie et ses dates de naissance et de mort sont très controversées. Les Arithmétiques...
-
ARTIN EMIL (1898-1962)
- Écrit par Jean-Luc VERLEY
- 1 319 mots
La part la plus importante de l'œuvre d'Artin concerne l'étude des corps de nombres algébriques etl'application des résultats obtenus à la théorie des nombres. Pour tout corps de nombres algébriques K, on peut considérer une fonction ζk(s), appelée la fonction zêta de Dedekind, qui... -
BAKER ALAN (1939-2018)
- Écrit par Bernard PIRE
- 338 mots
Alan Baker, mathématicien britannique, lauréat de la médaille Fields en 1970 pour ses travaux en théorie des nombres, est né le 19 août 1939 à Londres. Il a fait ses études supérieures à l'University College de Londres puis au Trinity College de Cambridge où il soutient sa thèse de doctorat en...
- Afficher les 55 références
Voir aussi
- GAUSS PÉRIODES DE, algèbre
- CONGRUENCE MODULO N
- NOMBRES PREMIERS
- IDÉAL, mathématiques
- FRACTIONNAIRE IDÉAL
- DEDEKIND ANNEAU DE
- CONJUGUÉ D'UN ÉLÉMENT
- EXTENSION, mathématiques
- NOMBRES ALGÉBRIQUES CORPS DE
- ALGÉBRIQUE ENTIER ou ENTIER RELATIF
- GALOIS GROUPE DE
- GAUSS ENTIER DE
- RACINE D'UNE ÉQUATION
- UNITÉ, mathématiques
- PREMIER IDÉAL
- NOMBRE IDÉAL
- CORPS DE CLASSES THÉORIE DU
- IDÉAUX CLASSES D'
- FERMAT GRAND THÉORÈME DE
- IDÈLES
- LEGENDRE SYMBOLE DE
- CORPS QUADRATIQUE
- RÉCIPROCITÉ QUADRATIQUE LOI DE
- PELL ÉQUATION DE
- RÉSIDU QUADRATIQUE
- RACINE PRIMITIVE
- CYCLOTOMIQUES ANNEAUX & CORPS
- NOMBRES ALGÉBRIQUES
- ADÈLES
- FONCTIONS ELLIPTIQUES & MODULAIRE
- DISCRIMINANT D'UN CORPS
- EULER-FERMAT THÉORÈME D'
- FROBENIUS AUTOMORPHISME DE
- HASSE HELMUT (1898-1979)
- GAUSS SOMMES DE
- BIQUADRATIQUE LOI DE RÉCIPROCITÉ
- MATHÉMATIQUES HISTOIRE DES