- 1. Convergences usuelles en analyse
- 2. Représentations par des intégrales
- 3. Représentations par des séries
- 4. Approximation par des suites
- 5. Interpolation et discrétisation
- 6. Opérations sur les représentations et les approximations
- 7. Stabilité et consistance
- 8. Optimisation de l'approximation ; rapidité de convergence
- 9. Bibliographie
FONCTIONS REPRÉSENTATION & APPROXIMATION DES
Approximation par des suites
Le problème de la représentation des fonctions comme limites de fonctions plus simples est intimement lié à celui de l' approximation des fonctions, qui ne relève pas uniquement de problèmes d'analyse numérique mais constitue un mode de représentation utile dans des questions d'ordre théorique : problèmes d'existence et d'unicité, démonstration de théorèmes par passage à la limite (argument de densité...). Les procédés d'approximations sont très divers ; nous avons retenu cinq méthodes importantes.
Méthodes convolutives
On utilise l'effet régularisant de la convolution : si f est une fonction peu régulière et si ϕ est très régulière, alors f * ϕ est aussi régulière que ϕ. En introduisant une approximation de l'unité, c'est-à-dire une suite (ϕn) de fonctions très régulières convergeant vers la mesure de Dirac δ (cf. supra, chap. 2), on approche f par des fonctions très régulières f * ϕn = fn.
Le fait que les fonctions ϕn soient à valeurs positives joue ici un rôle essentiel. Ce procédé d'approximation est particulièrement intéressant : en effet, lorsque f est de classe Cp, non seulement fn converge vers f, mais, pour tout k ≤ p, les dérivés Dkfn convergent vers Dkf. En prenant pour ϕn des fonctions C∞ à support compact, on obtient la densité des fonctions C∞ dans la plupart des espaces fonctionnels classiques et même des espaces de distributions ; ainsi, pour tout ouvert U de Rn, l'espace vectoriel D(U) des fonctions de classe C∞ dans U à support compact est dense dans l'espace vectoriel K(U) des fonctions continues à support compact contenu dans U.
En prenant pour ϕn des fonctions polynomiales, on obtient une démonstration du théorème d'approximation polynomiale de Weierstrass ; on peut prendre par exemple le noyau de Landau :
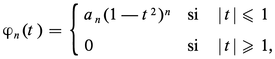
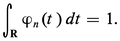
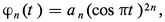
On notera que, en revanche, le noyau de Dirichlet (cf. séries trigonométriques, chap. 1) ne convient pas pour toutes les fonctions continues, ce qui se traduit par le fait que la série de Fourier d'une fonction continue peut diverger ; cela tient au fait que ce noyau n'est pas positif. Mais la convergence a bien lieu si la fonction est suffisamment régulière, c'est-à-dire si le module de continuité (cf. infra, chap. 7) décroît assez vite.
Méthodes de troncature
Il s'agit d'approcher des fonctions définies sur un ouvert U de Rn par des fonctions à support compact contenu dans U. À cet effet, on utilise une suite exhaustive (Kn) de compacts de U (cf. supra, chap. 1) et on construit une troncature universelle, c'està-dire une suite (χn) de fonctions telles que 0 ≤ χn ≤ 1, χn = 1 sur Kn et χn+1 = 0 en dehors de Kn+1.
On approche alors f par la suite fn = f χn.
Dans des questions d'intégration, on peut prendre pour χn la fonction caractéristique de Kn. Dans d'autres problèmes, il faut opérer moins brutalement. Par exemple, en prenant χn continue, on prouve que l'espace vectoriel K(U) des fonctions continues à support compact contenu dans U est dense dans l'espace vectoriel C0(U) des fonctions continues tendant vers 0 au bord de U (muni de la norme de la convergence uniforme) ou encore dans l'espace L2(U) des classes de fonctions de carré intégrable dans U (muni de la norme quadratique).
De même, on peut prendre χn de classe C∞ ; on prouve alors que l'espace vectoriel D(R) des fonctions de classe C∞ à support compact est dense dans l'espace vectoriel S(R) des fonctions[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
Écrit par
- Jean-Louis OVAERT : agrégé de l'Université, ancien élève de l'École normale supérieure, professeur de mathématiques spéciales
- Jean-Luc VERLEY : maître de conférences honoraire à l'université de Paris-VII
Classification
Médias
Graphe de f pour
Encyclopædia Universalis France
Graphe de f pour
Encyclopædia Universalis France
Fonction à oscillation rapide
Encyclopædia Universalis France
Autres références
-
DARBOUX GASTON (1842-1917)
- Écrit par Jacques MEYER
- 320 mots
Mathématicien français, né à Nîmes et mort à Paris. Après des études à l'École normale supérieure, Darboux fut l'assistant de J. Bertrand à la chaire de physique mathématique au Collège de France (1866-1867), puis enseigna au lycée Louis-le-Grand (1867-1872) et à l'École normale...
-
DÉRIVÉES PARTIELLES (ÉQUATIONS AUX) - Analyse numérique
- Écrit par Claude BARDOS et Martin ZERNER
- 5 849 mots
- 7 médias
Du point de vue mathématique, les méthodes d'éléments finis sont une sous-famille des méthodes de Ritz-Galerkin. Pour les problèmes variationnels, ces méthodes consistent à remplacer l'espace V des fonctions admissibles par un de ses sous-espaces VN dit « espace d'approximation ». -
DIFFÉRENTIELLES ÉQUATIONS
- Écrit par Christian COATMELEC , Encyclopædia Universalis et Maurice ROSEAU
- 11 635 mots
..., ..., yn), suite finie de n + 1 nombres réels telle que :où :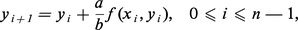
ce problème Pn est obtenu en divisant I = [x0, x0 + a]en n parties égales avec un pas égal à h = a/n et en cherchant uneapproximation yi de y(xi) où y est la solution (lorsqu'elle est unique) de P1.
-
GELFOND ALEXANDRE OSSIPOVITCH (1906-1968)
- Écrit par Jean-Luc VERLEY
- 156 mots
Mathématicien russe, né à Saint-Pétersbourg et mort à Moscou. Le nom de Gelfond reste attaché à l'étude des nombres transcendants ; on lui doit aussi d'importants résultats sur l'interpolation et l'approximation des fonctions de variable complexe. Depuis 1931, Gelfond a enseigné les mathématiques...
- Afficher les 14 références
