- 1. Convergences usuelles en analyse
- 2. Représentations par des intégrales
- 3. Représentations par des séries
- 4. Approximation par des suites
- 5. Interpolation et discrétisation
- 6. Opérations sur les représentations et les approximations
- 7. Stabilité et consistance
- 8. Optimisation de l'approximation ; rapidité de convergence
- 9. Bibliographie
FONCTIONS REPRÉSENTATION & APPROXIMATION DES
Article modifié le
Interpolation et discrétisation
Position du problème
Ce sont les problèmes de tabulation numérique des fonctions transcendantes élémentaires (lignes trigonométriques, logarithmes) et, à partir du xviie siècle, le calcul approché des intégrales et des dérivées qui ont été à l'origine du développement des méthodes interpolatoires. D'autre part, dans de nombreux phénomènes continus intervenant en sciences physiques, décrits par exemple à l'aide d'une fonction, on ne connaît les valeurs de cette fonction qu'en un certain nombre de points qui correspondent aux mesures effectuées. Les problèmes issus de l'astronomie, en particulier la détermination de la trajectoire des planètes, ont aussi joué un rôle moteur, comme en témoignent notamment les travaux d'Euler, Lagrange, Legendre, Laplace et Gauss.
Dans tous les cas, le phénomène continu est remplacé par un phénomène discret. Plus précisément, supposons que le phénomène continu est décrit par une fonction numérique f d'une variable réelle. On se donne une subdivision S de l'intervalle [α, β], c'està-dire une suite croissante (α0, α1, ..., αn) de points de [α, β] ; le module de la subdivision S est le nombre :
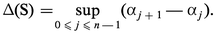
Lorsque α0 = α, αn = β et, pour tout j, αj+1 − αj = (β − α)/n, on dit que la subdivision est à pas constant, et Δ(S) = (β − α)/n s'appelle le pas de S.
Dans ces conditions, on associe à S la suite finie (f (α0), ..., f (αn)). Nous dirons qu'il s'agit d'une discrétisation de f (cf. analyse numérique). Le problème est alors de savoir dans quelle mesure on peut reconstituer f à partir des phénomènes discrétisés associés. À cet effet, on interpole la suite précédente par une fonction simple, par exemple une fonction polynomiale que nous noterons PS(f ), de degré ≤ n, prenant aux points αj les mêmes valeurs que f. Dans le cas où S est à pas constant, cette méthode a été élaborée dès le xviie siècle, notamment par Newton et Gregory, dans le cadre du calcul des différences finies (cf. infra). L'étude du cas général a été ébauchée par Newton et reprise par Lagrange, Cauchy et Hermite.
Il s'agit alors d'estimer la différence f − PS(f ), par exemple en majorant N∞(f − PS(f )), et d'étudier l'influence de la taille de l'intervalle [α, β], du choix de S et de la régularité de f sur la qualité de l'approximation. Il arrive souvent qu'on ne s'intéresse pas directement à f mais à la valeur d'une forme linéaire sur f. Pour ce type de problème, d'autres normes s'imposent : norme N1 pour les intégrales, normes f ↦ N∞(f ) + N∞(Df ) pour les dérivées. Dans les phénomènes physiques, les normes N2 interviennent souvent au titre de l'énergie.
On peut aussi se demander s'il est possible de reconstituer f comme limite de fonctions PS(f ) en raffinant les subdivisions, c'est-àdire en faisant tendre le module Δ(S) vers 0. Mais cette question présente des difficultés (cf. infra, Interpolation polynomiale). C'est pourquoi on a recours à un procédé plus élaboré : on se donne f sur un intervalle[a, b], on découpe cet intervalle en p intervalles de longueur (b − a)/p et, sur chacun de ces intervalles notés [α, β], on approche f par PS(f ). Le problème est alors de savoir comment on peut jouer sur les entiers n et p pour obtenir des approximations efficaces. Dans ce schéma plus élaboré, f est approchée sur[a, b]par une fonction ϕ continue et polynomiale par morceaux. On peut imposer en outre à ϕ des conditions de régularité plus fortes aux p − 1 points de subdivision de[a, b], ce qui conduit par exemple à la théorie des fonctions spline (cf. infra, Interpolation polynomiale par morceaux). Les méthodes de discrétisation[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
Écrit par
- Jean-Louis OVAERT : agrégé de l'Université, ancien élève de l'École normale supérieure, professeur de mathématiques spéciales
- Jean-Luc VERLEY : maître de conférences honoraire à l'université de Paris-VII
Classification
Médias
Graphe de f pour
Encyclopædia Universalis France
Graphe de f pour
Encyclopædia Universalis France
Fonction à oscillation rapide
Encyclopædia Universalis France
Autres références
-
DARBOUX GASTON (1842-1917)
- Écrit par Jacques MEYER
- 320 mots
Mathématicien français, né à Nîmes et mort à Paris. Après des études à l'École normale supérieure, Darboux fut l'assistant de J. Bertrand à la chaire de physique mathématique au Collège de France (1866-1867), puis enseigna au lycée Louis-le-Grand (1867-1872) et à l'École normale...
-
DÉRIVÉES PARTIELLES (ÉQUATIONS AUX) - Analyse numérique
- Écrit par Claude BARDOS et Martin ZERNER
- 5 850 mots
- 7 médias
Du point de vue mathématique, les méthodes d'éléments finis sont une sous-famille des méthodes de Ritz-Galerkin. Pour les problèmes variationnels, ces méthodes consistent à remplacer l'espace V des fonctions admissibles par un de ses sous-espaces VN dit « espace d' approximation ». -
DIFFÉRENTIELLES ÉQUATIONS
- Écrit par Christian COATMELEC , Encyclopædia Universalis et Maurice ROSEAU
- 11 637 mots
..., ..., yn), suite finie de n + 1 nombres réels telle que :où :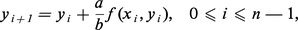
ce problème Pn est obtenu en divisant I = [x0, x0 + a]en n parties égales avec un pas égal à h = a/n et en cherchant une approximation yi de y(xi) où y est la solution (lorsqu'elle est unique) de P1.
-
GELFOND ALEXANDRE OSSIPOVITCH (1906-1968)
- Écrit par Jean-Luc VERLEY
- 165 mots
Alexandre Ossipovitch Gelfond est un mathématicien russe, né à Saint-Pétersbourg en 1906 et mort à Moscou en 1968. Le nom de Gelfond reste attaché à l'étude des nombres transcendants ; on lui doit aussi d'importants résultats sur l'interpolation et l'approximation des fonctions de variable complexe....
- Afficher les 14 références
Voir aussi
- CONVOLUTION PRODUIT DE
- LIMITE PROJECTIVE
- CONVERGENCE, mathématiques
- NORME, mathématiques
- LIMITE INDUCTIVE
- PRODUIT HERMITIEN
- PROJECTEUR, mathématiques
- FRACTION CONTINUÉE
- FOURIER SÉRIE DE
- APPLICATION RÉGULIÈRE
- CONVERGENCE DOMINÉE THÉORÈME DE LA
- CAUCHY FORMULE INTÉGRALE DE
- WEIERSTRASS THÉORÈME D'APPROXIMATION DE
- TAYLOR SÉRIE DE
- RADON MESURE DE
- SÉRIES ENTIÈRES
- FOURIER TRANSFORMATION DE
- HAAR THÉORÈME DE
- NOYAU, analyse mathématique
- APPROXIMATIONS SUCCESSIVES MÉTHODES DES
- ASCOLI THÉORÈME D'
- CAUCHY PROBLÈME DE
- SUITES, mathématiques
- DIRAC FONCTION DE
- CALCUL DIFFÉRENTIEL & INTÉGRAL
- ESCALIER FONCTION EN
- LAPLACE TRANSFORMATION DE
- ESPACE COMPLET
- ESPACE COMPACT
- BANACH-STEINHAUS THÉORÈME DE
- STABILITÉ, analyse numérique
- INTERPOLATION, mathématiques
- DUALITÉ, mathématiques
- RÉPONSE IMPULSIONNELLE
- CONSISTANCE, analyse numérique
- CONVERGENCE UNIFORME
- CONVERGENCE EN MOYENNE
- CONVERGENCE EN MOYENNE QUADRATIQUE
- CONVERGENCE SIMPLE
- CONVERGENCE RAPIDITÉ DE
- DISCRÉTISATION, mathématiques
- EULER MÉTHODE DU PAS À PAS D', analyse numérique
- DIFFÉRENCES CALCUL DES
- DINI THÉORÈME DE
- LAGRANGE INTERPOLATION DE
- HERMITE INTERPOLATION DE
- FUBINI THÉORÈME DE
- POISSON ÉQUATION DE
- QUASI ANALYTIQUE
- NOYAU INTÉGRAL
- NEWTON POLYNÔMES DE
- SOBOLEV ESPACE DE
- SOLUTION ÉLÉMENTAIRE
- SÉRIES DE FONCTIONS
- TCHEBYCHEV POLYNÔME DE
- SPLINE FONCTION
- APPROXIMATION
- EXPONENTIELLE FONCTION
- REPRÉSENTATION INTÉGRALE
