- 1. Convergences usuelles en analyse
- 2. Représentations par des intégrales
- 3. Représentations par des séries
- 4. Approximation par des suites
- 5. Interpolation et discrétisation
- 6. Opérations sur les représentations et les approximations
- 7. Stabilité et consistance
- 8. Optimisation de l'approximation ; rapidité de convergence
- 9. Bibliographie
FONCTIONS REPRÉSENTATION & APPROXIMATION DES
Optimisation de l'approximation ; rapidité de convergence
Optimisation de l'approximation
Avec les notations du chapitre précédent, nous allons étudier les deux problèmes suivants :
a) l'unicité de l'élément ϕn de En optimisant l'approximation de f par les éléments de En ; il est alors intéressant de construire des méthodes explicites de calcul de ϕn ;
b) la distance δn(f ) tend-elle vers 0 si n tend vers + ∞ ? Si oui, déterminer la vitesse de convergence en fonction des propriétés de f.
Voici deux exemples classiques.
Dans le premier, E est un espace vectoriel de fonctions 1-périodiques à valeurs complexes et En est le sous-espace vectoriel Tn des polynômes trigonométriques de degré ≤ n, c'est-à-dire des combinaisons linéaires des fonctions exponentielles t ↦ e2iπpt, où |p| ≤ n.
Dans le second, E est un espace vectoriel de fonctions définies sur[a, b]et En est le sous-espace vectoriel Pn des polynômes de degré ≤ n.
Bien entendu, les réponses aux problèmes précédents vont dépendre du type de convergence considéré. Nous examinerons principalement le cas des normes N2 (approximation en moyenne quadratique) et N∞ (approximation uniforme).
Unicité de ϕn
Théorème 1. L'unicité de ϕn est assurée lorsque la boule unité est strictement convexe, c'est-à-dire si les relations ∥x∥ = ∥y∥ = 1 et αx + βy = 1 avec α > 0, β > 0, α + β = 1 impliquent x = y.
Cette dernière condition est réalisée pour l'espace E = L2(μ) des fonctions de carré intégrable pour une mesure μ muni de la norme N2, et, plus généralement, pour les espaces Lp(μ) pour 1 < p < + ∞. Elle ne l'est pas pour l'espace L1(μ), ni pour l'espace E = C([a, b]) muni de la norme N∞ ; on peut relier ce phénomène à la forme des boules de R2 pour ces mêmes normes (cf. figure in espaces vectoriels normés). D'ailleurs, dans ces deux cas, on peut donner des exemples où il n'y a pas unicité de ϕn : il suffit par exemple de prendre E = C([0, 1]) muni de la norme N∞. Si E0 est la droite vectorielle engendrée par la fonction t ↦ t, alors d(1, E0) est atteinte pour toutes les fonctions ϕ(t ) = αt où 0 ≤ α ≤ 2. Il en est de même si E est l'espace C(T) des fonctions continues 1-périodiques et si E0 est la droite vectorielle engendrée par la fonction t ↦ sin2 πt. Cela tient au fait que toutes les fonctions de E0 s'annulent en un même point.
Ainsi, le problème de l'unicité de la meilleure approximation uniforme dans E = C([a, b]) est assez délicat. Pour le résoudre, on introduit le concept de sous-espace vectoriel régulier de fonctions (cf. supra, chap. 5).
On a alors le théorème suivant, dû à Haar.
Théorème 2. Soit En un sous-espace vectoriel de C([a, b]), ou de l'espace vectoriel C(T) des fonctions continues 1-périodiques, muni de la norme de la convergence uniforme. Il est équivalent de dire :
a) En est régulier ;
b) l'unicité de ϕn est assurée pour tout élément f de C([a, b]) (ou de C(T)).
Ce théorème s'applique à la meilleure approximation polynomiale uniforme des fonctions continues, car le sous-espace vectoriel des fonctions polynômes de degré ≤ n est régulier. Il s'applique aussi à la meilleure approximation uniforme des fonctions continues périodiques par les polynômes trigonométriques, car le sous-espace vectoriel des polynômes trigonométriques de degré ≤ n est lui aussi régulier.
Caractérisation et calcul explicite de ϕn
Théorème 3 (cas des normes quadratiques). Soit En un sous-espace vectoriel de dimension finie d'un espace vectoriel hilbertien E. Alors ϕn n'est autre que la projection orthogonale de f sur En ; autrement dit, ϕn = pn(f ), où pn est le projecteur orthogonal sur En. En[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
Écrit par
- Jean-Louis OVAERT : agrégé de l'Université, ancien élève de l'École normale supérieure, professeur de mathématiques spéciales
- Jean-Luc VERLEY : maître de conférences honoraire à l'université de Paris-VII
Classification
Médias
Graphe de f pour
Encyclopædia Universalis France
Graphe de f pour
Encyclopædia Universalis France
Fonction à oscillation rapide
Encyclopædia Universalis France
Autres références
-
DARBOUX GASTON (1842-1917)
- Écrit par Jacques MEYER
- 320 mots
Mathématicien français, né à Nîmes et mort à Paris. Après des études à l'École normale supérieure, Darboux fut l'assistant de J. Bertrand à la chaire de physique mathématique au Collège de France (1866-1867), puis enseigna au lycée Louis-le-Grand (1867-1872) et à l'École normale...
-
DÉRIVÉES PARTIELLES (ÉQUATIONS AUX) - Analyse numérique
- Écrit par Claude BARDOS et Martin ZERNER
- 5 849 mots
- 7 médias
Du point de vue mathématique, les méthodes d'éléments finis sont une sous-famille des méthodes de Ritz-Galerkin. Pour les problèmes variationnels, ces méthodes consistent à remplacer l'espace V des fonctions admissibles par un de ses sous-espaces VN dit « espace d'approximation ». -
DIFFÉRENTIELLES ÉQUATIONS
- Écrit par Christian COATMELEC , Encyclopædia Universalis et Maurice ROSEAU
- 11 635 mots
..., ..., yn), suite finie de n + 1 nombres réels telle que :où :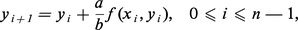
ce problème Pn est obtenu en divisant I = [x0, x0 + a]en n parties égales avec un pas égal à h = a/n et en cherchant uneapproximation yi de y(xi) où y est la solution (lorsqu'elle est unique) de P1.
-
GELFOND ALEXANDRE OSSIPOVITCH (1906-1968)
- Écrit par Jean-Luc VERLEY
- 156 mots
Mathématicien russe, né à Saint-Pétersbourg et mort à Moscou. Le nom de Gelfond reste attaché à l'étude des nombres transcendants ; on lui doit aussi d'importants résultats sur l'interpolation et l'approximation des fonctions de variable complexe. Depuis 1931, Gelfond a enseigné les mathématiques...
- Afficher les 14 références
