MARTINGALES THÉORIE DES

Calcul stochastique

Considérons l'équation :

représentant, par exemple, l'évolution d'un système où intervient un bruit blanc modélisé par la « dérivée » d'un mouvement brownien (B_t), t ≥ 0 ; pour donner un sens à (⋆), on a besoin de définir l'intégrale du type :

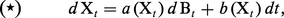
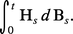
L'intégrale stochastique. Lorsque (H_t), t ≥ 0, est un processus convenable et (X_t), t ≥ 0, une semi-martingale, on peut définir :

car si H_t = 1_{{t ≤ T}}, où T est un temps d'arrêt, la seule définition naturelle est :

ensuite, par linéarité et continuité, cette « intégrale stochastique » se prolonge à tout H borné, mesurable par rapport à la tribu engendrée par les (H_t), t ≥ 0 de la forme ci-dessus ; on montre que ce prolongement n'est possible que si (X_t), t ≥ 0 est une semi-martingale ; lorsque (X_t) est à variation finie, l'intégrale stochastique coïncide avec l'intégrale de Stieltjes ; mais, lorsque (X_t), t ≥ 0, n'est pas à variation finie (par exemple si (X_t), t ≥ 0, est une martingale continue), l'intégrale de Stieltjes n'existe pas alors que l'intégrale stochastique est définie. Indiquons deux outils essentiels qui permettent de manier cette intégrale :

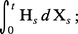
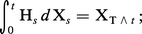
– un théorème de convergence dominée qui s'exprime ainsi : Si une suite (H_tⁿ), t ≥ 0, de processus intégrables converge simplement vers un processus (H_t), t ≥ 0, et si, pour tout t ≥ 0, H_tⁿ est majorée en valeur absolue par K_t où (K_t), t ≥ 0, est un processus intégrable, alors on a, au sens de la convergence en probabilité,

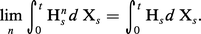
– une formule de changement de variable (due à K. Ito dans le cas du mouvement brownien), qui permet de développer tout un calcul différentiel stochastique. Lorsque (X_t), t ≥ 0, est une semi-martingale continue de décomposition X_t = A_t + M_t où (M_t), t ≥ 0, est localement une martingale continue, la « formule de Ito » a la forme suivante, F désignant une fonction de variables réelles admettant des dérivées F′, F″ continues :

la première intégrale est une intégrale stochastique, la seconde une intégrale de Stieltjes définie à partir du processus croissant « variation quadratique de M » à savoir ([M]_t), t≥ 0.

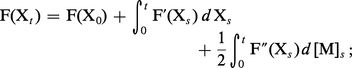
Reprenons maintenant l'équation différentielle stochastique (⋆). On peut en définir plusieurs types de solutions :

– soient (Ω, F, p), (B_t, F_t), t ≥ 0, donnés : une solution forte de (⋆) est un processus (X_t), t ≥ 0, qui vérifie (⋆).

– soient (Ω, F), (X_t, F_t), t ≥ 0, donnés ; une solution faible de (⋆) est un processus (B_t), t ≥ 0, et une probabilité p sur (Ω, F) tels que (B_t, F_t), t ≥ 0, soit un mouvement brownien sur (Ω, F, p), avec (⋆) vérifiée.

On peut montrer que trouver les solutions faibles de (⋆) revient à résoudre le problème des martingales X = {Y, Z} où :

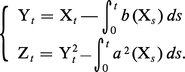
Lorsque les coefficients a et b sont lipschitziens (lorsqu'ils vérifient la condition |a(x′) − a(x″)| ≤ K|x′ − x″| sur une certaine constante K > 0, et pour x′ et x″ quelconques, et de même pour b), (⋆) admet une solution forte ; mais, sans hypothèse de Lipschitz, on n'a pas nécessairement de solution forte.

Lorsque a et b satisfont à des conditions de régularité moins fortes que celle de Lipschitz (par exemple : b mesurable borné, a continu borné), l'équation admet une solution faible unique (X_t), t ≥ 0.

Rappelons que, à temps continu, on appelle (comme dans le cas du temps discret) processus de Markov une famille de variables aléatoires (X_t), t ≥ 0, qui « oublie le passé », c'est-à-dire telle que p(X_t ∈ A|FX_s) = p(X_t ∈ A|X_s) pour tous s ≤ t, et pour tout A mesurable dans l'espace des états. On définit alors les probabilités de transition :

et les opérateurs :

qui forment un semi-groupe, c'est-à-dire :

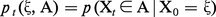
On appelle générateur infinitésimal du processus l'opérateur défini par :

Sous certaines conditions naturelles, cette limite existe pour toutes les fonctions assez régulières (deux fois différentiables, par exemple si E = R^d).

Mais on peut voir aussi que, toujours sous des conditions raisonnables, on peut reconstituer le processus à partir de son générateur infinitésimal A ; disons cela autrement : à partir du comportement du processus pour t infiniment petit, on peut retrouver l'ensemble du processus.

On peut alors montrer que la solution de l'équation différentielle stochastique ci-dessus (⋆) est un processus de Markov dont le générateur infinitésimal a la forme :

La réciproque est d'ailleurs vraie : si (X_t), t ≥ 0, est un processus de Markov de générateur infinitésimal (⋆⋆), alors (X_t), t ≥ 0, est solution faible de l'équation différentielle (⋆).

Historiquement, les équations différentielles stochastiques ont été développées dans le cadre de la théorie des processus de Markov ; ensuite, le développement de la théorie de l'intégrale stochastique a permis de considérer des équations différentielles stochastiques plus générales que (⋆), dont les solutions ne sont pas des processus de Markov.

Une application de l'étude de l'équation (⋆) est la résolution de l'équation aux dérivées partielles ordinaire (c'est-à-dire non stochastique) :

dont la solution est :

où (Xt) et p sont solutions faibles de l'équation (⋆).

Remarquons enfin que, comme dans le cas du mouvement brownien (exemple 8), un processus de Markov à temps continu du type ci-dessus, de coefficients a et b, peut être obtenu comme limite d'une suite de processus de Markov de saut.