TRESSES, mathématiques

Peignage des tresses pures

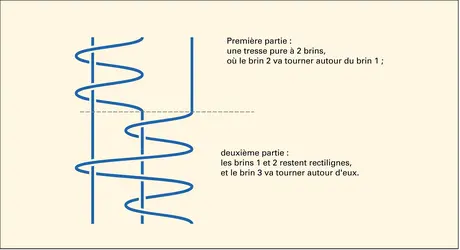
C'est en partant directement des tresses géométriques qu'Artin a fourni la première solution au problème d'isotopie. Notons d'abord que, si les permutations associées à deux mots de tresses w et w' diffèrent, alors certainement w ≡ w' est faux. On en déduit que, pour résoudre le problème d'isotopie générale, il suffit de savoir reconnaître si un mot de tresse w codant une tresse pure représente ou non la tresse triviale. L'effacement du n-ième brin dans une tresse pure à n brins fournit une tresse pure à n-1 brins, et il en résulte que toute tresse pure à n brins peut s'écrire de façon unique comme le produit d'une tresse pure à n-1 brins (avec un n-ième brin non tressé) et d'une tresse où le n-ième brin va faire des tours autour des n-1 premiers brins qui restent rectilignes (fig. 17). Cette décomposition exprime que le groupe P_n est un produit semi-direct du groupe P_n-1 et d'un groupe libre à n-1 générateurs, et on peut en déduire une solution du problème d'isotopie, un mot de tresse pur w représentant la tresse triviale si son peignage aboutit au mot vide.

La théorie de Garside

L'étude algébrique des groupes de tresses part de la présentation d'Artin et repose sur le fait que B_n est le groupe de fractions d'un monoïde intéressant.

On a vu que le groupe B_n admet la présentation:

(*)

.

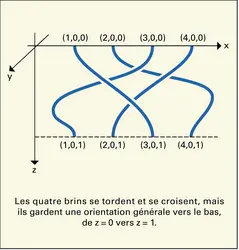
Alors le monoïde B_n⁺ de présentation (*) se plonge dans B_n et il correspond aux tresses où tous les croisements ont même orientation. De plus, B_n est groupe de fractions de B_n⁺: tout élément de B_n est quotient de deux éléments de B_n⁺. Un rôle majeur est joué par la tresse Δ_n, dont le carré engendre le centre de B_n pour n ∗ 3 (fig. 18).

Disons qu'une tresse b₁divise une tresse b₂ s'il existe b dans B_n⁺ vérifiant b₂ = b₁b, et appelons simple toute tresse divisant Δ_n dans B_n⁺. Il existe n! tresses simples à n brins, et toute tresse positive admet un diviseur simple maximal. En itérant, on obtient pour chaque tresse de B_n une unique expression Δ_n^kb₁…b_l avec k entier relatif, b₁, …, b_l simples distinctes de Δ_n et b_i diviseur simple maximal de b_ib_i+1 pour chaque i. De là, on déduit une solution au problème d'isotopie: partant de deux mots de tresses w et w', on peut déterminer les expressions normales des tresses représentées par w et w', et on a alors w ≡ w' si et seulement si ces expressions coïncident. Cette méthode reflète ce qu'on appelle une structure automatique sur B_n, et sa complexité est quadratique: pour chaque n, il existe une constante c_n telle que le calcul de la forme normale d'un mot de tresse à n brins de ℓ lettres requière c_nl² étapes au plus.

La théorie de Garside permet également de résoudre le problème de conjugaison des tresses, c'est-à-dire, étant donnés deux mots de tresse quelconques w et w', de déterminer si les tresses représentées par w et w' sont conjuguées dans le groupe B_n.

Propriétés d'ordre

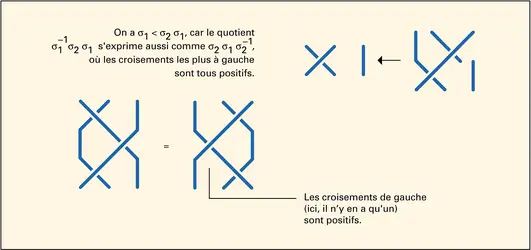
L'étude des liens entre tresses et autodistributivité mène naturellement à ordonner les tresses. Étant donné deux tresses b et b', déclarons b < b' vrai si, parmi les différents mots représentant la tresse b^-1b', il en existe au moins un où, pour un certain i, figure la lettre σ_i, mais ni σ_i^–1, ni aucune lettre  σ_j^±1 avec j < i (fig. 19). On montre que la relation < est un ordre total sur B_n, compatible avec le produit à gauche (Dehornoy). Le groupe B_n est donc ordonnable, et il[...]