VARIÉTÉS DIFFÉRENTIABLES

Sous-variétés de E_n

La notion de sous-variété de E_n est une généralisation de la notion de surface introduite dans l'article géométrie différentielle classique. On dit qu'un sous-ensemble localement fermé V de E_n est une sous-variété de dimension p si, pour tout point x de V, il existe un ouvert U de E_p et une application continue :

Soit f une fonction numérique définie sur un ouvert Ω de la variété V de classe C^k (on suppose que Ω est l'intersection de V et de l'ouvert O de E_n) et soit r ≤ k ; alors, les deux conditions suivantes sont équivalentes.

1. Il existe une fonction numérique F de classe C^r définie sur O telle que f soit la restriction de F à Ω.

2. Pour toute carte différentiable (U, ϕ), la fonction numérique f ∘ ϕ définie sur ϕ⁻¹(Ω) est de classe C^r.

Une telle fonction f est appelée une fonction de classe C^r définie sur l'ouvert Ω de la variété V de classe C^k, avec k ≥ r.

Systèmes de cartes et fonctions différentiables

Dans la condition 2 ci-dessus, le fait que V soit un sous-ensemble de E_n n'intervient pas. Il doit donc être possible de définir des fonctions différentiables sur un espace topologique quelconque en se donnant un système de cartes ; c'est ce que l'on va faire.

Soit V un espace topologique séparé ; on dira que l'on s'est donné un « système de cartes de dimension p qui est C^k-compatible » sur V si l'on s'est donné un recouvrement de V par des ouverts V_i, pour i ∈ I, et, pour tout i, un homéomorphisme ϕ_i d'un ouvert U_i de E_p sur V_i de telle façon que la condition (C) suivante soit vérifiée.

(C) Pour tout couple (i, j) tel que V_i∩V_j soit non vide, l'application :

est de classe C^k.

Soit f une fonction numérique définie sur un ouvert Ω de V ; on dira que f est de classe C^r, pour r ≤ k, si cette fonction vérifie la condition (C′) suivante.

(C′) Quelle que soit la carte (U_i, ϕ_i) telle que U_i∩ Ω ≠ ∅, l'application :

est de classe C^r.

La condition (C) implique que, si l'on a Ω ⊂ V_i∩ V_j, l'application f ∘ ϕ_i est de classe C^r si et seulement si f ∘ ϕ_j est de classe C^r. Cela assure que l'ensemble des fonctions de classe C^r au voisinage d'un point x de V a des propriétés analogues à celles de l'ensemble des fonctions de classe C^r au voisinage d'un point de E_p. Si l'on n'avait pas imposé cette condition (C), il n'en serait pas ainsi ; il se pourrait même que les seules fonctions vérifiant la condition (C′) soient les fonctions constantes.

Structure de variété

Les fonctions numériques de classe C^r, avec r ≤ k, sur un ouvert Ω de V forment un anneau de fonctions ; notons C^r_Ω cet anneau. Pour tout ouvert Ω′ contenu dans Ω, la restriction des fonctions définit un homomorphisme de C^r_Ω′ dans C^r_Ω. On obtient ainsi un faisceau d'anneaux sur V (cf. topologie - Topologie algébrique, chap. 7). Par définition, une variété de classeC^r et de dimension p est un espace topologique séparé sur lequel sont donnés des faisceaux d'anneaux C¹, ..., C^k, qui peuvent être définis par la méthode que l'on vient de décrire. Les cartes ne sont qu'un outil pour définir ces faisceaux de fonctions ; en particulier, deux systèmes de cartes C^k-compatibles qui définissent le même faisceau des fonctions de classe C^r, pour tout r ≤ k, sont deux façons de définir la même variété.

Exemples

Il est clair que tout ouvert de E_n est muni naturellement d'une structure de variété de dimension n qui peut être définie par une seule carte. Les surfaces régulières telles qu'elles sont définies dans l'article géométrie différentielle classique et, plus généralement, les sous-variétés de classe C^k de E_n sont des variétés différentiables. Citons quelques exemples classiques de variétés.

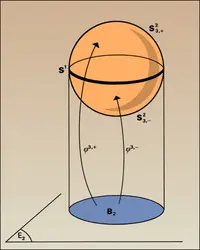
La sphère de dimension n

Une sphère de dimension n est, par définition, l'ensemble Sⁿ de points de E_n+1 dont les coordonnées (x₁, ..., x_n+1) sont liées par la relation x²₁ + ... + x²_n+1 = 1. C'est une sous-variété de classe C∞ et de dimension n de E_n+1. En effet, soit :

la boule unité ouverte de E_n. Pour tout i, avec 1 ≤ i ≤ n + 1, on définit deux applications ϕ^i,+ et ϕi,− de B_n dans E_n+1, en posant :

on voit que ϕ^i,+ réalise un homéomorphisme de B_n sur la partie Sⁿ_i,+ de Sⁿ dont la i-ème coordonnée est strictement positive et que ϕ^i,− réalise un homéomorphisme de B_n sur la partie Sⁿ_i,− de Sⁿ dont la i-ème coordonnée est strictement négative.

Les applications ϕ^i,+ et ϕ^i,− sont de classe C∞ et leurs différentielles sont toujours de rang n. Il en résulte que les 2 (n + 1) applications ϕ^i,+ et ϕ^i,− donnent un système de cartes pour Sⁿ.

Dans le cas n = 2, on obtient ainsi un système de six cartes pour la sphère S²⊂ E₃ représentant les hémisphères x > 0, x < 0, y > 0, y < 0, z > 0 et z < 0. On aurait pu définir la même structure de variété sur la sphère S² avec deux cartes en utilisant deux projections stéréographiques de pôle (0, 0, 1) et de pôle (0, 0, − 1) respectivement (cf. fonctions analytiques - Représentation conforme, chap. 3 et fig. 8).

Les espaces projectifs

Dans l'article topologie - Topologie générale, à la fin du chapitre 1, on trouvera la définition de l' espace projectif réel P_n(R) de dimension n dont les points sont les droites de Rⁿ⁺¹ qui passent par l'origine. Pour définir la topologie, on associe à tout sous-espace affine U de Rⁿ⁺¹ qui ne passe pas par l'origine une injection :

où ϕ_U(u) est la droite de Rⁿ⁺¹ qui passe par u et par l'origine. On peut vérifier que les couples (U, ϕ_U) forment un système de cartes C∞-compatibles. Donc P_n(R) est une variété de classe C∞ et de dimension n ; c'est une variété abstraite, c'est-à-dire qu'elle n'est pas, de manière naturelle, une sous-variété d'un espace E_n.

Une construction analogue permet de définir un système de cartes sur l'espace projectif complexe P_n(C) des sous-espaces vectoriels de dimension complexe 1 de Cⁿ⁺¹. Ces cartes sont aussi C∞-compatibles ; elles identifient des ouverts de P_n(C) à des sous-espaces de dimension complexe n de Cⁿ⁺¹ ; donc P_n(C) est une variable de classe C∞ et de dimension 2 n.

Le groupe spécial orthogonal SO(3)

On appelle groupe spécial orthogonal SO(3) le groupe des isométries directes de l'espace E₃ qui conservent un point. C'est encore le groupe multiplicatif des matrices réelles carrées d'ordre 3, inversibles, dont l'inverse est égal à la transposée et dont le déterminant est positif. Ce groupe est utilisé depuis longtemps en mécanique dans l'étude des mouvements d'un solide dont un point est fixe. Il existe un voisinage U de zéro dans l'espace vectoriel des matrices antisymétriques réelles d'ordre 3 et un voisinage Ω de l'identité dans SO(3) tels que l'exponentielle matricielle :

définisse un homéomorphisme de U sur Ω. On a donc une carte (U, ϕ) telle que ϕ(U) = Ω soit un voisinage de l'identité. Pour tout point M de SO(3), on définit une carte (U, ϕ_M) telle que ϕ_M(U) soit un voisinage de M, en posant ϕ_M(A) = M ( ϕ(A) pour tout point A de U. On vérifie que toutes ces cartes forment un système C∞-compatible ; par conséquent SO(3) est une variété de classe C∞ et de dimension 3.

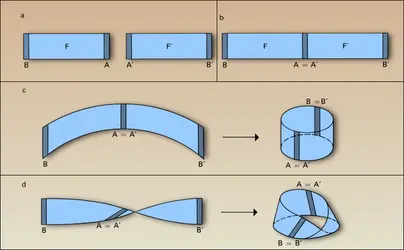
Cylindre et bande de Möbius

Considérons deux rectangles, par exemple les deux bandes de papier de la figure a ; on va les recoller pour faire une variété de dimension 2. On recolle d'abord A à A′, puis on recolle B à B′. Il y a deux façons de le faire : on peut recoller le bord supérieur au bord supérieur et le bord inférieur au bord inférieur et on obtient un cylindre ; on peut aussi tordre la feuille de façon à recoller le bord supérieur droit au bord inférieur gauche et le bord supérieur gauche au bord inférieur droit : on obtient une variété appelée bande de Möbius. Remarquons que la bande de Möbius n'a qu'une seule face : si les deux feuilles de papier sont rouges d'un côté et bleues de l'autre et si l'on a recollé A à A′ en respectant les couleurs, le recollement de B à B′ ne les respecte pas.

Application de classe C^k

Soit U₁ et U₂ des ouverts de E_n et E_p ; une application continue f : U₁→ U₂ est de classe C^r si et seulement si, pour toute fonction numérique η de classe C^r définie sur un ouvert Ω de U₂, la fonction η ∘ f, définie sur l'ouvert f ⁻¹(Ω) de U₁, est de classe C^r. Par analogie, si V et W sont des variétés de classe C^k, on dit qu'une application continue f de V dans W est de classe C^r, avec r ≤ k, si, pour tout ouvert Ω de W et pour toute fonction numérique η de classe C^r définie sur Ω, la fonction numérique η ∘ f, définie sur l'ouvert f ⁻¹(Ω) de V, est de classe C^r. On démontre que :

Les variétés de classe C^k et les applications de classe C^r, avec r ≤ k, forment une catégorie ; les isomorphismes de cette catégorie sont appelés les difféomorphismes de classe C^r. Un difféomorphisme de classe C^r de V sur W est donc un homéomorphisme f de V sur W tel que, pour tout ouvert O de V, la correspondance η ↦ η ∘ f soit une bijection de l'ensemble des fonctions numériques de classe C^r définies sur f (O), sur l'ensemble des fonctions numériques de classe C^r définies sur O.

Sous-variétés

Le théorème des fonctions implicites permet de donner deux nouvelles caractérisations des sous-variétés de E_n. Un sous-espace fermé V de E_n est une sous-variété de dimension p et de classe C^k s'il vérifie l'une des deux conditions équivalentes suivantes.

(C₁) Pour tout point x de V, il existe un voisinage ouvert Ω de x dans E_n et une application η de classe C^k de Ω dans E_n−p qui est de rang n − p en tout point de Ω et telle que Ω ∩ V soit l'image inverse par η d'un point de E_n−p.

(C₂) Pour tout point x de V, il existe un voisinage ouvert Ω de x dans E_n et un difféomorphisme μ de classe C^k de Ω sur un ouvert O de E_n tels que μ(Ω ∩ V) = O ∩ E_p.

Plus généralement, si V est un fermé de la variété W de classe C^k et de dimension n, on dit que V est une sous-variété de dimension p et de classe C^k de W si la condition suivante est vérifiée.

(C′₂) Pour tout point x de V, il existe un voisinage ouvert Ω de x dans W et un difféomorphisme μ de classe C^k de Ω sur un ouvert O de E_n tels que μ(Ω ∩ V) = O ∩ E_p.

Les applications :

Si l'on regarde les exemples donnés plus haut, on constate que, pour p < n, la sphère S^p est une sous-variété de Sⁿ, l'espace projectif réel P_p(R) est une sous-variété de l'espace P_n(R) et l'espace projectif complexe P_p(C) est une sous-variété de P_n(C). On remarquera aussi que la caractérisation des sous-variétés de E_n par la condition (C₁) montre que SO(3) est une sous-variété de E₉ (qui s'identifie à l'espace vectoriel des matrices carrées d'ordre 3) puisque l'équation ^tMM = I est équivalente à une équation F(M) = O, où F est une application de classe C∞ de E₉ dans E₆, qui est de rang 6 au voisinage de chaque point de SO(3).

Variétés à bord

Soit V une variété de classe C^k et de dimension n et soit X un fermé de V dont la frontière (c'est-à-dire l'ensemble des points de X dont tous les voisinages rencontrent X et V − X) est une sous-variété de dimension n − 1 et de classe C^k de V : on dit que X est une variété à bord de dimension n et de classe C^k et la frontière de X est appelée le bord de X.

Dans une variété à bord de dimension n, tout point non situé sur le bord a un voisinage difféomorphe à un ouvert de Rⁿ et tout point situé sur le bord a un voisinage difféomorphe à un voisinage de R₊ⁿ, en désignant par R₊ⁿ le fermé de Rⁿ formé des points dont la dernière coordonnée est positive ou nulle. Ainsi, la boule unité Dⁿ de Rⁿ (pour la distance euclidienne) est une variété à bord dont le bord est la sphère Sⁿ⁻¹. La demi-sphère S₊ⁿ = R₊ⁿ⁺¹∩ Sⁿ est une variété à bord, de bord Sⁿ⁻¹ (cf. dans le cas n = 3).