Abonnez-vous à Universalis pour 1 euro

VARIÉTÉS DIFFÉRENTIABLES

Article modifié le

Formes différentielles

Une forme différentielle de degré p est un tenseur de type (0, p) antisymétrique, c'est-à-dire tel que, quels que soient les champs (X1, ..., Xp) et la permutation σ de {1, ..., p}, de signature ε(σ), on ait :

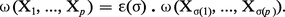
Les formes différentielles de degré 1 sont les formes de degré 1 que l'on vient de définir au chapitre 3. Les formes de degré 2 sont les tenseurs de type (0, 2) tels que l'on ait ω(X, Y) = − ω(Y, X). Les formes de degré p constituent un module sur l'anneau C∞ ; on le notera ∧p. On peut aussi considérer les formes différentielles de degré p comme les sections de classe C∞ d'un fibré dont la fibre en m est la composante de degré p de l'algèbre extérieure du dual de l'espace tangent en m (cf. algèbrelinéaire, chap. 6). On en déduit que, pour p supérieur à la dimension de la variété, toute forme différentielle de degré p est nulle.

Produit extérieur

Le produit extérieur de la forme ω de degré p et de la forme ω′ de degré q est, par définition, la forme de degré p + q :

où la sommation est effectuée sur toutes les permutations σ des entiers {1, 2, ..., p + q}.

On sait que toute carte (U, ϕ) de la variété V de dimension n donne une base dx1, ..., dxn du module ∧1(ϕ(U)) des formes différentielles de degré 1 définies sur ϕ(U). Pour p > 1, les formes de degré p qui s'écrivent :

avec 1 ≤ i1 < i2 < ... < ip ≤ n, constituent une base du module ∧p(ϕ(U)) des formes différentielles de degré p définies sur ϕ(U) ; donc toute forme différentielle ω de degré p définie sur ϕ(U) s'écrit :
où les ai sont des fonctions de classe C∞, la sommation étant faite sur l'ensemble des multi-indices i = (i1, ..., ip) tels que 1 ≤ i1 < ... < ip ≤ n.

Abonnez-vous à Universalis pour 1 euro

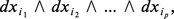
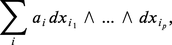
Si f : W → V est une application de classe C∞, à la forme :

définie sur ϕ(U) on associe la forme :
où Fi est la i-ième fonction coordonnée de l'application composée :
on dit que f *(ω) est l'image inverse de ω par f.

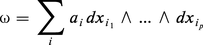
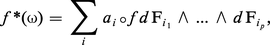
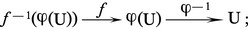
Intégration des formes différentielles

Soit X une sous-variété compacte à bord de dimension n d'une variété V de dimension n (il se peut que le bord de X soit vide et même que X = V). Considérons une carte (U, ϕ) de V telle que :

et une forme ω de degré n sur V, qui est nulle en dehors d'un compact K contenu dans ϕ(U). La forme ω s'écrit :
si (U′, ϕ′) est une autre carte telle que ϕ′(U′) contienne K, la forme ω s'écrit également :
on voit facilement que, pour tout point M de K, α′(M) est le produit de α(M) par le déterminant de la différentielle de ϕ-1 ∘ ϕ′ au point ϕ′−1(M). Il en résulte que l'on a :
  c'est-à-dire que ces intégrales n-ièmes sont égales au signe près. Plus précisément, si K est connexe, le signe du déterminant de la différentielle de ϕ-1 ∘ ϕ′ est constant sur K ; s'il est positif, les deux intégrales sont égales et, s'il est négatif, elles sont opposées.

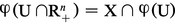
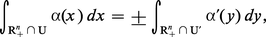
Si V est orientée au voisinage de K, on peut décider de n'employer que des cartes compatibles avec cette orientation ; alors la quantité :

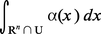
est indépendante de la carte choisie ; on l'appelle l'intégrale de ω sur X et on utilise la notation ∫Xω.

Soit maintenant une forme quelconque ω de degré n sur V et soit (Ui, ϕi), avec i ∈ I, une famille finie de cartes de V dont les images recouvrent X. On peut montrer qu'il existe une famille de fonctions numériques (fi), avec i ∈ I, telle que, pour tout i, la fonction fi soit nulle en dehors d'un compact Ki contenu dans ϕi(Ui) et que, pour tout point M de X, on ait :

une telle famille de fonctions est appelée une partition de l'unité au-dessus de X, relative au recouvrement (ϕi(Ui)), avec i ∈ I. Pour tout i, on a déjà défini :
puisque fiω est nulle en dehors de Ki ; on pose alors :
ce qui définit l'intégrale sur X de la forme ω.

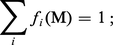
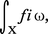
Formules de Stokes

À toute forme ω de degré p on associe une forme dω, de telle façon que l'on ait :

La forme dω est appelée la dérivée extérieure de ω ; il est clair que, si, au-dessus de ϕ(U), on a :

alors on a :

Abonnez-vous à Universalis pour 1 euro

On voit que le degré de dω est supérieur d'une unité à celui de ω.

Pour toute sous-variété Y orientée de la variété V et pour toute forme ω sur V dont le degré est égal à la dimension de Y, l'intégrale :

où i est l'injection de Y dans V et i*(ω) l'image directe de ω par i, est appelée l'intégrale de ω sur Y. La formule de Stokes s'écrit alors de la façon suivante : soit Y une sous-variété orientée de dimension p de V et soit dY le bord de Y ; pour toute forme ω de degré p − 1 sur V, on a :

Le signe des deux membres de cette égalité dépend des orientations choisies sur Y et dY ; elle ne peut donc être vraie que si ces orientations sont correctement reliées entre elles. Avec les définitions que l'on a données, il faut que, si (X1, ..., Xn−1) est une base orientée de T(dY)M et si Xn est un vecteur sortant au point M, les vecteurs (X1, ..., Xn) soient une base orientée de T(Y)M.

Formes différentielles sur E3

Le plus souvent, quand on travaille avec la variété E3, on munit ses espaces tangents du produit scalaire habituel. Alors, à tout champ de vecteurs X on associe une forme ωX de degré 1, en posant, pour tout champ Y et pour tout point m,

produit scalaire des deux vecteurs X(m) et Y(m). Cette correspondance est bijective, si bien que, inversement, à toute forme de degré 1 correspond un champ de vecteurs.

De même, à tout champ X on associe une forme τX de degré 2, en posant, pour tout point m.

où ∧ désigne le produit vectoriel usuel sur E3. Cette correspondance est également bijective. On voit alors facilement que le rotationnel du champ T est le champ X tel que τX soit la dérivée de la forme ωT. De même, la divergence de X correspond à la différentielle de la forme τX (cf. calcul infinitésimal -Calcul à plusieurs variables, chap. 1). C'est ainsi que, si df est la différentielle d'une fonction différentielle f, il lui correspond le vecteur gradient de f, dont les composantes sur la base canonique sont :
avec :

Accédez à l'intégralité de nos articles

  • Des contenus variés, complets et fiables
  • Accessible sur tous les écrans
  • Pas de publicité

Découvrez nos offres

Déjà abonné ? Se connecter

Écrit par

Carte mentale
Élargissez votre recherche dans Universalis

Classification

Médias

Carte de la sphère S2 - crédits : Encyclopædia Universalis France

Carte de la sphère S2

Encyclopædia Universalis France

Cylindre et bande de Möbius - crédits : Encyclopædia Universalis France

Cylindre et bande de Möbius

Encyclopædia Universalis France

Courbe de longueur minimum - crédits : Encyclopædia Universalis France

Courbe de longueur minimum

Encyclopædia Universalis France

Afficher les 7 médias de l'article VARIÉTÉS DIFFÉRENTIABLES

Autres références

  • CALCUL INFINITÉSIMAL - Calcul à plusieurs variables

    • Écrit par
    • 5 445 mots
    Les « images » et « noyaux » des applications différentiables satisfaisant aux énoncés précédents sont localement des morceaux de «  variétés différentiables », qui devront être convenablement recollés pour aboutir à une théorie globale.

  • COSMOLOGIE

    • Écrit par
    • 9 302 mots
    • 6 médias
    Fond diffus cosmologique - crédits : NASA
    ...propriétés structurales inhabituelles de cette géométrie. Les mathématiciens appellent variété, et plus particulièrement, dans le cas qui nous occupe, variété différentiable ou riemannienne, un tel espace généralisé. On peut dire que la variété espace-temps est aussi complexe (et donc riche en structures),...

  • DONALDSON SIMON KIRWAN (1957- )

    • Écrit par
    • 331 mots

    Mathématicien britannique, lauréat de la médaille Fields en 1986. Né le 20 août 1957 à Cambridge (Grande-Bretagne), Simon Kirwan Donaldson fait ses études supérieures au Pembroke College de Cambridge et au Worcester College d'Oxford où il soutient sa thèse de doctorat en 1983. Il occupe ensuite...

  • ESPACE, mathématique

    • Écrit par
    • 1 671 mots
    Ces considérations prennent une extension considérable en 1846 dans le mémoire d'habilitation de Bernhard Riemann.Riemann, loin de se restreindre à considérer des surfaces dans l'espace, introduit des objets de dimension quelconque (qu'on appelle aujourd'hui variétés différentielles...
  • Afficher les 18 références

Voir aussi

Abonnez-vous à Universalis pour 1 euro

Rejoignez-nous

Inscrivez-vous à notre newsletter